Question

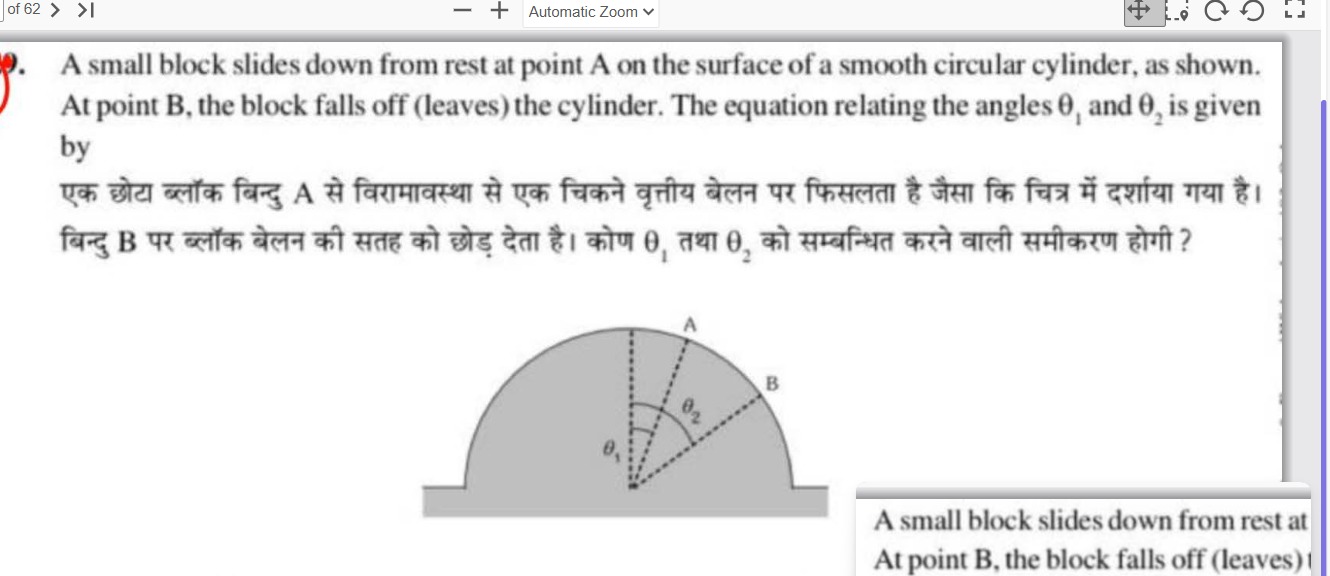
A small block slides down from rest at point A on the surface of a smooth circular cylinder, as shown. At point B, the block falls off (leaves) the cylinder. The equation relating the angles $\theta_1$ and $\theta_2$ is given by

एक छोटा ब्लॉक बिन्दु A से विरामावस्था से एक चिकने वृत्तीय बेलन पर फिसलता है जैसा कि चित्र में दर्शाया गया है। बिन्दु B पर ब्लॉक बेलन की सतह को छोड़ देता है। कोण $\theta_1$ तथा $\theta_2$ को सम्बन्धित करने वाली समीकरण होगी ?

Answer 1

2 \cos \theta_1 = 3 \cos \theta_2

Answer 2

The problem involves a small block sliding down a smooth circular cylinder from rest at point A and leaving the cylinder at point B. We need to find the relationship between the angles $\theta_1$ (position of A) and $\theta_2$ (position of B), both measured from the vertical axis. Let $R$ be the radius of the cylinder and $m$ be the mass of the block.

1. Conservation of Mechanical Energy (from A to B): The block starts from rest at A, so its initial velocity $v_A = 0$. Let's set the potential energy reference at the center of the cylinder.

• At point A:
  • Potential Energy $PE_A = mgR \cos \theta_1$.
  • Kinetic Energy $KE_A = 0$.
  • Total Energy $E_A = mgR \cos \theta_1$.
• At point B:
  • Potential Energy $PE_B = mgR \cos \theta_2$.
  • Let $v_B$ be the velocity of the block at B.
  • Kinetic Energy $KE_B = \frac{1}{2} mv_B^2$.
  • Total Energy $E_B = mgR \cos \theta_2 + \frac{1}{2} mv_B^2$.

Since the surface is smooth (frictionless), mechanical energy is conserved: $E_A = E_B$ $mgR \cos \theta_1 = mgR \cos \theta_2 + \frac{1}{2} mv_B^2$ Rearranging to find $v_B^2$: $\frac{1}{2} mv_B^2 = mgR (\cos \theta_1 - \cos \theta_2)$ $v_B^2 = 2gR (\cos \theta_1 - \cos \theta_2)$ (Equation 1)

2. Newton's Second Law at point B (where the block leaves the cylinder): At point B, the forces acting on the block are:

• Gravitational force $mg$ acting vertically downwards.
• Normal force $N$ acting radially outwards.

For circular motion, the net radial force provides the centripetal force $mv_B^2/R$. The component of gravity along the radius towards the center is $mg \cos \theta_2$. Applying Newton's second law in the radial direction: $mg \cos \theta_2 - N = \frac{mv_B^2}{R}$

The block leaves the cylinder when the normal force $N$ becomes zero. Setting $N=0$: $mg \cos \theta_2 = \frac{mv_B^2}{R}$ Rearranging to find $v_B^2$: $v_B^2 = gR \cos \theta_2$ (Equation 2)

3. Relating $\theta_1$ and $\theta_2$: Equate the expressions for $v_B^2$ from Equation 1 and Equation 2: $2gR (\cos \theta_1 - \cos \theta_2) = gR \cos \theta_2$ Divide both sides by $gR$: $2 (\cos \theta_1 - \cos \theta_2) = \cos \theta_2$ $2 \cos \theta_1 - 2 \cos \theta_2 = \cos \theta_2$ $2 \cos \theta_1 = 3 \cos \theta_2$

This is the equation relating the angles $\theta_1$ and $\theta_2.