Question

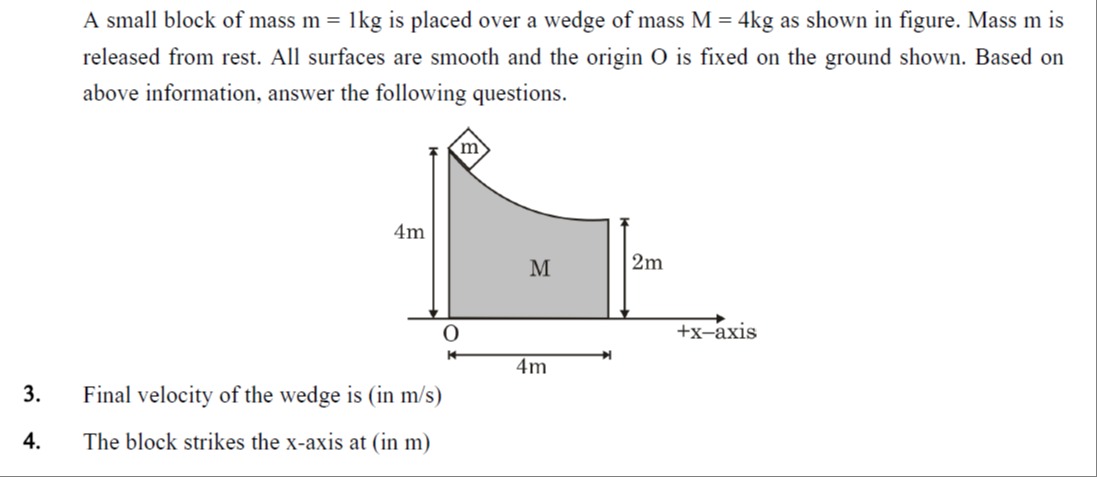
A small block of mass m = 1kg is placed over a wedge of mass M = 4kg as shown in figure. Mass m is released from rest. All surfaces are smooth and the origin O is fixed on the ground shown. Based on above information, answer the following questions.

3. Final velocity of the wedge is (in m/s)
4. The block strikes the x-axis at (in m)

Answer 1

sqrt{2}, 4 - 8/sqrt{5}

Answer 2

The problem is a bit ambiguous regarding the initial position of the block and the shape of the curved surface. However, assuming the block slides down the curved surface and leaves the wedge horizontally at height 2m, and the conservation laws are applicable, we can solve for the final velocity of the wedge and the trajectory of the block.

Let $m = 1$ kg and $M = 4$ kg. Initially, the system is at rest. The initial height of the block is $h_i = 4$ m. When the block leaves the wedge, its height is $h_f = 2$ m.
Let $v_M$ be the final velocity of the wedge (in the horizontal direction) and $v_m$ be the velocity of the block when it leaves the wedge.
Since there are no external horizontal forces, the total horizontal momentum is conserved. Initially, the momentum is 0. Let $v_{m,x}$ be the horizontal velocity of the block and $v_{m,y}$ be the vertical velocity of the block when it leaves the wedge. The velocity of the wedge is $v_M$ in the horizontal direction.
Conservation of horizontal momentum: $mv_{m,x} + Mv_M = 0$.

Since all surfaces are smooth, mechanical energy is conserved.
Initial energy: $E_i = K_i + U_i = 0 + mgh_i = mg(4)$.
Final energy: $E_f = K_f + U_f = \frac{1}{2}m(v_{m,x}^2 + v_{m,y}^2) + \frac{1}{2}Mv_M^2 + mgh_f = \frac{1}{2}m(v_{m,x}^2 + v_{m,y}^2) + \frac{1}{2}Mv_M^2 + mg(2)$.
Conservation of energy: $E_i = E_f$
$mg(4) = \frac{1}{2}m(v_{m,x}^2 + v_{m,y}^2) + \frac{1}{2}Mv_M^2 + mg(2)$
$2mg = \frac{1}{2}m(v_{m,x}^2 + v_{m,y}^2) + \frac{1}{2}Mv_M^2$.

From the figure, it is implied that the block leaves the wedge at the point where the height is 2m and the surface of the wedge is horizontal. This means that the velocity of the block relative to the wedge is horizontal at this point. Since the wedge is moving horizontally, the vertical component of the block's velocity relative to the ground is zero at this instant, i.e., $v_{m,y} = 0$.

With $v_{m,y} = 0$, the energy equation becomes:
$2mg = \frac{1}{2}mv_{m,x}^2 + \frac{1}{2}Mv_M^2$.
From momentum conservation, $v_{m,x} = -\frac{M}{m}v_M$.
Substitute into the energy equation:
$2mg = \frac{1}{2}m(-\frac{M}{m}v_M)^2 + \frac{1}{2}Mv_M^2$
$2mg = \frac{1}{2}m\frac{M^2}{m^2}v_M^2 + \frac{1}{2}Mv_M^2$
$2mg = \frac{M^2}{2m}v_M^2 + \frac{M}{2}v_M^2 = \frac{M}{2}v_M^2 (\frac{M}{m} + 1) = \frac{M}{2}v_M^2 \frac{M+m}{m}$
$4m^2g = M(M+m)v_M^2$
$v_M^2 = \frac{4m^2g}{M(M+m)}$
$v_M = \sqrt{\frac{4m^2g}{M(M+m)}} = \frac{2m}{\sqrt{M(M+m)}}\sqrt{g}$.

Using the given values: m=1kg, M=4kg, g=10 m/s$^2$.
$v_M = \sqrt{\frac{4(1)^2(10)}{4(4+1)}} = \sqrt{\frac{40}{4(5)}} = \sqrt{\frac{40}{20}} = \sqrt{2}$ m/s.

So, the final velocity of the wedge is $\sqrt{2}$ m/s.

Now, let's find the horizontal velocity of the block when it leaves the wedge:
$v_{m,x} = -\frac{M}{m}v_M = -\frac{4}{1}\sqrt{2} = -4\sqrt{2}$ m/s.
The block leaves the wedge at height $y_0 = 2$m with initial velocity $\vec{v}_0 = -4\sqrt{2} \hat{i}$.
Let's assume the block leaves the wedge at the right end of the wedge's base, which is at $x_0 = 4$m from the origin O.
The motion of the block after leaving the wedge is projectile motion under gravity.
The equations of motion are:
$x(t) = x_0 + v_{0x}t = 4 - 4\sqrt{2}t$
$y(t) = y_0 + v_{0y}t - \frac{1}{2}gt^2 = 2 + 0t - \frac{1}{2}(10)t^2 = 2 - 5t^2$

The block strikes the x-axis when $y(t) = 0$.
$2 - 5t^2 = 0 \implies 5t^2 = 2 \implies t^2 = \frac{2}{5} \implies t = \sqrt{\frac{2}{5}}$ s (since t > 0).

The x-coordinate where the block strikes the x-axis is:
$x = 4 - 4\sqrt{2}t = 4 - 4\sqrt{2}\sqrt{\frac{2}{5}} = 4 - 4\sqrt{\frac{4}{5}} = 4 - 4 \times \frac{2}{\sqrt{5}} = 4 - \frac{8}{\sqrt{5}}$
$x = 4 - \frac{8}{\sqrt{5}} = 4 - \frac{8\sqrt{5}}{5}$.
Using $\sqrt{5} \approx 2.236$, $x \approx 4 - \frac{8 \times 2.236}{5} = 4 - \frac{17.888}{5} = 4 - 3.5776 = 0.4224$.

Let's recheck the assumption about the initial x-coordinate. The figure shows the base of the wedge from O to 4m. The block starts from the top. It is possible that the block leaves the wedge at the right end of the horizontal part, which is at x=4m.

Final Answer Check:
Question 3: Final velocity of the wedge is $\sqrt{2}$ m/s.
Question 4: The block strikes the x-axis at $4 - \frac{8}{\sqrt{5}}$ m.