Question

A small block of mass $1kg$ is released from rest at the top of a rough track. The track is mentioned to be a circular arc having a radius $40m$. The block slides without topping along the track. A frictional force is acting on it in the direction opposite in the instantaneous velocity. The work done in overcoming the friction up to the point Q as represented in the figure below will be $150J$. (Take the acceleration due to gravity $g=10m{{s}^{-2}}$)

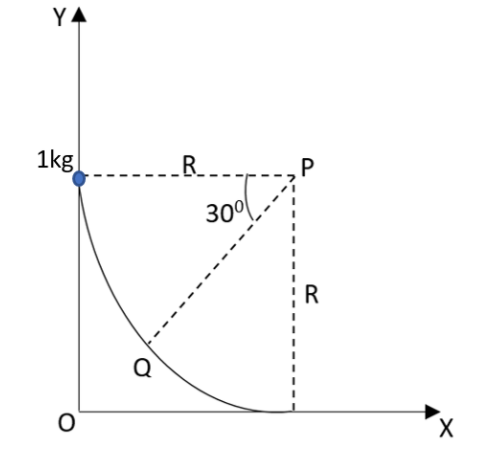
$\begin{aligned} & A.7.5N \\\ & B.8.6N \\\ & C.11.5N \\\ & D.22.5N \\\ \end{aligned}$

Answer 1

Resolve the gravitational force vector into cosine and sine parts. Then find out the centripetal force provided by the system. The centripetal force can be found by taking the ratio of the product of the mass and square of velocity to the radius of the circular arc. Calculate the loss in potential energy and find the kinetic energy possessed by the particle also. Calculate the normal force using this.

Complete step by step answer:
the weight vector can be resolved as,

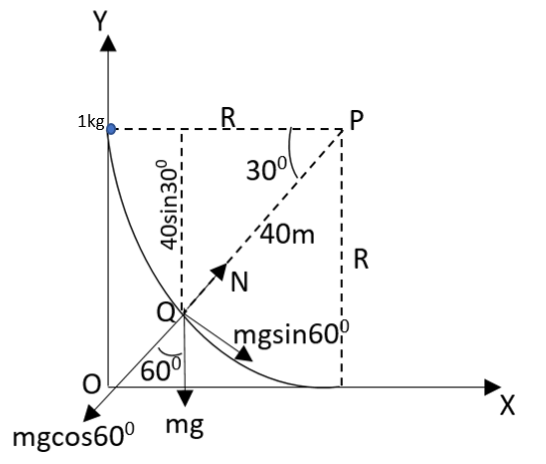
The centripetal force acting can be found by the equation,
$N-mg\cos 60{}^\circ =\dfrac{m{{v}^{2}}}{t}$
Rearranging this equation will give,
$N=mg\cos 60{}^\circ +\dfrac{m{{v}^{2}}}{t}$
The loss in potential energy can be found as,
$\text{loss in P}\text{.E=mg+40sin30}{}^\circ \text{=200J}$
The work done in overcoming the friction has been given as,
$w=1.5J$
The kinetic energy possessed by the particle will be written as,
$KE=50J$
The kinetic energy is found by taking the product of half of the mass of the block and the square of the velocity. This can be shown in equation as,
$\dfrac{1}{2}m{{v}^{2}}=50J$
Rearranging this equation will give,
$m{{v}^{2}}=100J$
Substitute all these values obtained in the equation of the centripetal force. That is we can write that,
$N=1\times 10\times \dfrac{1}{2}+\dfrac{100}{40}$
Let us simplify this equation as,
$N=5+2.5=7.5N$

So, the correct answer is “Option A”.

Note: The normal force is defined as the force that surfaces will be providing in order to oppose the solid bodies from passing through each other. Normal force is defined as a contact force. Suppose that any two surfaces are not in contact, they won’t provide a normal force on each other.