Question
Question: A small block of mass 0.1kg lies on a fixed inclined plane PQ which makes an angle \[\theta \] with ...
A small block of mass 0.1kg lies on a fixed inclined plane PQ which makes an angle θ with the horizontal. A horizontal force of 1N acts on the block through its center of mass as shown in the figure. The block remains stationary if (let g=10ms−2):
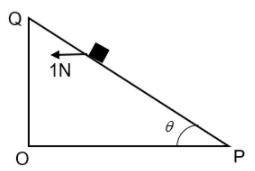
Solution
The block will be at rest on the inclined plane only if the frictional force acting on it equals the component of normal reaction of the block. We have to resolve the forces into its components and see at what angle the frictional force will be sufficient.
Complete answer:
Let us resolve the different forces acting on the block.
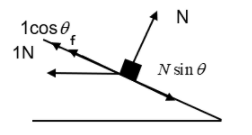
From the above diagram, it is clear that the net force acting the block on the inclined plane should be zero for it to be at rest. The forces acting on the body are the Normal Reaction (N), the frictional force (f) and the horizontal force (1N). A component of each of these forces are acting with the frictional force. So the balancing condition of these forces gives a particular angle, at which the block may start sliding down.
Let us equate the forces acting in the direction of the frictional force, f.
i.e.,
f−Nsinθ+1cosθ=0
