Question

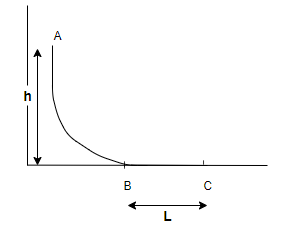
A small ball of mass m starts at a point A with speed ${v_0}$​ and moves along a frictionless track AB as shown. The track BC has coefficient of friction $\mu$. The ball comes to stop at C after travelling a distance $L$. Find $L$.

                                      ![](https://www.vedantu.com/question-sets/b17ddd05-2661-426c-8db2-8465a60619846204966420375356714.png)  

(A) $\dfrac{{2h}}{\mu } + \dfrac{{\mathop v\nolimits_0^2 }}{{2\mu g}}$
(B) $\dfrac{h}{\mu } + \dfrac{{\mathop v\nolimits_0^2 }}{{2\mu g}}$
(C) $\dfrac{h}{{2\mu }} + \dfrac{{\mathop v\nolimits_0^2 }}{{\mu g}}$
(D) $\dfrac{{4h}}{\mu } + \dfrac{{\mathop v\nolimits_0^2 }}{{2\mu g}}$

Answer 1

The given problem is an example of motion of a particle in frictionless and frictional track. As in this problem the particle is at some height $h$ and then starts moving along the given track from A to C and stops at C. So, this problem can be solved using the law of energy conservation.

Step-by-step solution:
Step 1: As in the question it is given that the particle starts moving from point A where track AB is frictionless and then from point B to C where track BC is frictional track with coefficient of friction$\mu$.
Let us consider that the initial velocity of the particle (say mass of the particle is $m$) is $\mathop v\nolimits_0$and initial height from which the particle starts moving along the given track, is $h$.

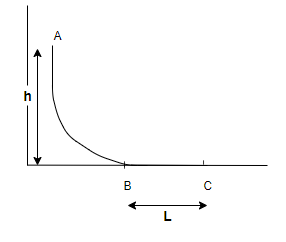
Step 2: From the above figure we can see that –
Total energy of the ball at point A will be equal to the sum of kinetic energy at that point and potential energy at that point. So, total energy can be written as –
Total energy at A = kinetic energy + potential energy
$\mathop {\left( {\mathop E\nolimits_t } \right)}\nolimits_A = \dfrac{1}{2}m\mathop v\nolimits_0^2 + mgh$ …………………………..(1)
We know that energy is conserved in any closed system so the total energy at point B will be –
$\mathop {\left( {\mathop E\nolimits_t } \right)}\nolimits_B = \dfrac{1}{2}m\mathop v\nolimits_0^2 + mgh$ …………………………..(2)
Step 3: Now, we know that friction opposes the relative motion of the ball so the energy that is at point B will be used against the work done by the frictional force while the particle is moving from point B to C.
But we know that frictional force is equal to the frictional coefficient $\mu$ times the normal force on the body (i.e., R).
So, $F = \mu R$; where $R = mg$, and $m =$ mass of the body, and $g =$acceleration due to gravity
$F = \mu mg$.........................................(3)
So, from the definition of work done against the frictional force –
$W = F \times S$; where $S = L =$distance covered by body from point B to C
Substituting the value from equation (3), we will get –
$W = \mu mgL$ …………………………...(4)
Now, from the energy conservation law –
$\mathop {\left( {\mathop E\nolimits_t } \right)}\nolimits_A$ or $\mathop {\left( {\mathop E\nolimits_t } \right)}\nolimits_B =$ $W$
So, from equation (2) and (4), we will get –
$\dfrac{1}{2}m\mathop v\nolimits_0^2 + mgh = \mu mgL$, on rearranging this equation
$L = \dfrac{h}{\mu } + \dfrac{{\mathop v\nolimits_0^2 }}{{2\mu g}}$

So, the correct option is (B).

Note:
-While solving these types of problems one should always remember that friction is a non-conservative force, i.e. work done against friction is path dependent.
-In the presence of friction, some energy is always lost in the form of heat etc. Because of the reason we can say mechanical energy is not conserved.