Question

A small ball of mass $2\times {{10}^{-3}}kg~$ having a charge of $1\mu C$ is suspended by a string of length 0.8 m. Another identical ball having the same charge is kept at the point of suspension. Determine the minimum horizontal velocity which should be imparted to the lower ball so that it can make a complete revolution.

Answer 1

We have to diagrammatically represent the given situation. Further, we have to analyse the mechanical and the electrostatic forces that act on the balls. Since it is suspended by a string, tension and gravitational force will exist and due to the presence of charge, electromagnetic force may also exist.

Formula Used:
Electrostatic force between two charged bodies $q_1$, $q_2$ separated at a distance r.
$F=\dfrac{k{{q}^{2}}}{r}$, where k is a constant.
Centripetal force F of a body with mass m and velocity v rotating in radius r
$F=\dfrac{m{{v}^{2}}}{r}$

Complete step by step answer:

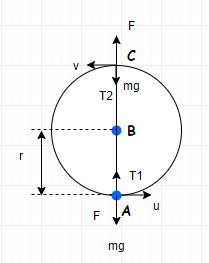
There are two balls in this circle created. The ball at the centre B and the ball at A
The ball at A experiences gravitational force downwards, and electrostatic force with the ball at the centre, in the upward direction. It also experiences tension $T_1$.
Gravitational force $F=mg$
Electrostatic force $=\dfrac{k{{q}^{2}}}{r}$
We can take the topmost point C as the critical point, where all the resultant forces act towards the centre. Here, the tension is zero.
We can say that the resultant at critical point is the centripetal force.
Hence,
$\Rightarrow \dfrac{m{{v}^{2}}}{r}=mg+{{T}_{2}}-\dfrac{k{{q}^{2}}}{r}$
Since T2 is zero,
\begin{aligned} & \dfrac{m{{v}^{2}}}{r}=mg-\dfrac{k{{q}^{2}}}{r} \\\ & \Rightarrow {{v}^{2}}=gr-\dfrac{k{{q}^{2}}}{mr}\\_\\_\\_\\_\\_\\_\\_\\_\\_\\_\\_(1) \\\ & \\\ \end{aligned}
When we take A as the reference point and apply law of conservation of energy,

& \dfrac{1}{2}m{{u}^{2}}=\dfrac{1}{2}m{{v}^{2}}+mg(2r) \\\ & \Rightarrow {{u}^{2}}={{v}^{2}}+4gr \\\ & \Rightarrow {{u}^{2}}-{{v}^{2}}=4gr\\_\\_\\_\\_\\_(2) \\\ \end{aligned}$$ Substituting (1) in (2) we get $\begin{aligned} & {{u}^{2}}=4gr+gr-\dfrac{k{{q}^{2}}}{mr} \\\ & u=\sqrt{5gr-\dfrac{k{{q}^{2}}}{mr}} \\\ & u=\sqrt{(5\times 10\times 0.8)-\dfrac{(9\times {{10}^{9}}){{10}^{-12}}}{(0.8)(2\times {{10}^{-3}})}} \\\ & u=5.86m/s \\\ \end{aligned}$ Hence, minimum horizontal velocity which should be imparted to the lower ball to make a complete revolution is 5.86m/s **Note:** While solving questions that involve systems with more than one force, the students can proceed with a free body diagram that denotes the directions of force from which, the correct answer can be deduced. If not, there are higher chances for an error.