Solveeit Logo
Login

Question

Question: A small ball falling vertically downward with constant velocity, \(v=2m/s\), strikes elastically an ...

A small ball falling vertically downward with constant velocity, v=2m/sv=2m/s, strikes elastically an inclined plane moving with velocity, 2m/s2m/s as shown in the figure. The velocity of rebound of the ball with respect to the ground is:

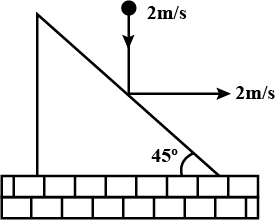
(a)4m/s(a)4m/s
(b)25m/s(b)2\sqrt{5}m/s
(c)22m/s(c)2\sqrt{2}m/s
(d)2m/s(d)2m/s

Explanation

Solution

By Conservation of Momentum, when the ball rebounds off the surface of the inclined plane elastically, it experiences same momentum but in the opposite direction so the net change in momentum is twice the initial momentum of the ball. We will also make use of the relative velocity of the ball with respect to the incline, it will help us visualize the problem better.

Complete answer:
Let the initial momentum of the ball be p.
Since the ball rebounds elastically, total change in momentum is =2p=2p.
Now, the Relative velocity of ball with respect to the incline is given by:
Before collision:
=−v=-v directed to the right (horizontal component)
=−v=-v directed upwards (vertical component)
After collision:
=+v=+v directed left (horizontal component)
=+v=+v directed downwards (vertical component)
Therefore, the Velocity of the rebound ball can be written as:
⇒Vrb,g=(2Vi^)2+(Vj^)2\Rightarrow {{V}_{rb,g}}=\sqrt{{{(2V\widehat{i})}^{2}}+{{(V\widehat{j})}^{2}}} [equation number (1)(1) ]
Where,
Vrb,g={{V}_{rb,g}}= velocity of rebound ball with respect to the ground
2Vi^=2V\widehat{i}= horizontal component of rebound ball velocity
Vj^=V\widehat{j}= vertical component of rebound ball velocity
Putting the values of each term in equation number (1)(1) , we get:
⇒Vrb,g=(2×2)2+(2)2m/s\Rightarrow {{V}_{rb,g}}=\sqrt{{{(2\times 2)}^{2}}+{{(2)}^{2}}}m/s
⇒Vrb,g=20m/s ⇒Vrb,g=25m/s \begin{aligned} & \Rightarrow {{V}_{rb,g}}=\sqrt{20}m/s \\\ & \Rightarrow {{V}_{rb,g}}=2\sqrt{5}m/s \\\ \end{aligned}
Hence, the rebound velocity of the ball is 25m/s2\sqrt{5}m/s .

Hence, option (b) is the correct option.

Note:
While solving these types of questions, we can choose the frame of reference according to our ease and the velocity of our frame of reference should be kept zero to help solve the question properly and quickly. Hence, making our calculations easier and faster.