Solveeit Logo
Login

Question

Question: A slob is subjected to two forces \({\vec F_1}\) and \({\vec F_2}\) of same magnitude F as shown in ...

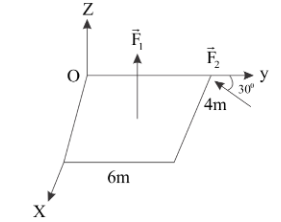
A slob is subjected to two forces F⃗1{\vec F_1} and F⃗2{\vec F_2} of same magnitude F as shown in the figure. Force F⃗2{\vec F_2} is in XY-plane while force F⃗1{\vec F_1} acts along Z-axis at the point (2i^+3j^)\left( {2\hat i + 3\hat j} \right). What will be the moment of these forces about point O?

(A) (3i^−2j^−3k^)F\left( {3\hat i - 2\hat j - 3\hat k} \right)F
(B) (3i^+2j^+3k^)F\left( {3\hat i + 2\hat j + 3\hat k} \right)F
(C) (3i^+2j^−3k^)F\left( {3\hat i + 2\hat j - 3\hat k} \right)F
(D) (3i^−2j^+3k^)F\left( {3\hat i - 2\hat j + 3\hat k} \right)F

Explanation

Solution

The moment of a force about a point can be found out by taking the cross product of the position vector of the point at which the force is being applied and the force vector. The total moment of two or more forces about a point is the sum of moments of individual forces about that point.

Complete step by step answer:
From the given figure, we can write the force vectors and the position vectors of the points at which these forces are acting. We obtain,
F⃗1=Fk^{\vec F_1} = F\hat k …equation (1)
r⃗1=2i^+3j^{\vec r_1} = 2\hat i + 3\hat j …equation (2)
F⃗2=(Fsin⁡30∘)(−i^)+(Fcos⁡30∘)(−j^)=−F2i^−3F2j^{\vec F_2} = \left( {F\sin 30^\circ } \right)\left( { - \hat i} \right) + \left( {F\cos 30^\circ } \right)\left( { - \hat j} \right) = - \dfrac{F}{2}\hat i - \dfrac{{\sqrt 3 F}}{2}\hat j…equation (3)
r⃗2=6j^{\vec r_2} = 6\hat j …equation (4)
The position vector is the vector to the point at the application of force with its tail at O.
The cross products of unit vectors are as follows,
i^×j^=k^\hat i \times \hat j = \hat k
⇒j^×i^=−k^\Rightarrow\hat j \times \hat i = - \hat k
⇒i^×i^=0\Rightarrow\hat i \times \hat i = 0
⇒j^×k^=i^\Rightarrow\hat j \times \hat k = \hat i
⇒k^×j^=−i^\Rightarrow\hat k \times \hat j = - \hat i
⇒j^×j^=0\Rightarrow\hat j \times \hat j = 0
⇒k^×i^=j^\Rightarrow\hat k \times \hat i = \hat j
⇒i^×k^=−j^\Rightarrow\hat i \times \hat k = - \hat j
⇒k^×k^=0\Rightarrow\hat k \times \hat k = 0
We now find the moment of force F⃗1{\vec F_1} about point O by taking the cross product of the position vector of the point at which this force is acting and the force itself. Using equation (1) and (2), we obtain,
τ⃗1=r⃗1×F⃗1=(2i^+3j^)×(Fk^)=3Fi^−2Fj^{\vec \tau _1} = {\vec r_1} \times {\vec F_1} = \left( {2\hat i + 3\hat j} \right) \times \left( {F\hat k} \right) = 3F\hat i - 2F\hat j …equation (5)
We now find the moment of force F⃗2{\vec F_2} about point O by taking the cross product of the position vector of the point at which this force is acting and the force itself. Using equation (3) and (4), we obtain,
τ⃗2=r⃗2×F⃗2=(6j^)×(−F2i^−3F2j^)=3Fk^{\vec \tau _2} = {\vec r_2} \times {\vec F_2} = \left( {6\hat j} \right) \times \left( { - \dfrac{F}{2}\hat i - \dfrac{{\sqrt 3 F}}{2}\hat j} \right) = 3F\hat k …equation (6)
The total moment acting about point O is the sum of the moments of forces F⃗1{\vec F_1} and F⃗2{\vec F_2} about that point. So, the total moment is,
τ⃗=τ⃗1+τ⃗2=3Fi^−2Fj^+3Fk^=(3i^−2j^+3k^)F\vec \tau = {\vec \tau _1} + {\vec \tau _2} = 3F\hat i - 2F\hat j + 3F\hat k = \left( {3\hat i - 2\hat j + 3\hat k} \right)F

Hence, the correct answer is option D..

Note: The moment of force is the cross product of distance and force. The order in which the distance and force are written in the formula for moment of force is important as interchanging their positions may give a different answer, leading to an incorrect solution.