Question

A slightly conical wire of length L and radii ${r_1}$and ${r_2}$ is stretched by two forces applied parallel to length in opposite directions and normal to end faces. If $Y$ denotes the young's modulus then the elongation of the wire is
$(A)\dfrac{{FL}}{{2\pi {r_1}{r_2}Y}}$
$(B)\dfrac{{FL}}{{\pi {r_1}{r_2}Y}}$
$(C)\dfrac{{2FL}}{{\pi {r_1}{r_2}Y}}$
$(D)\dfrac{{4FL}}{{\pi {r_1}{r_2}Y}}$

Answer 1

Here, the total length of the conical wire before the extension is $L$ and the ${r_1}$and ${r_2}$ are the radii of the conical wire. We are going to find the elongation of the wire when it was stretched by two equal and parallel forces acting in opposite directions. Young’s modulus is defined as the ratio of stress due to the applied load to longitudinal strain. We are going to derive the elongation of the wire with the young’s modulus formula.

Complete answer:

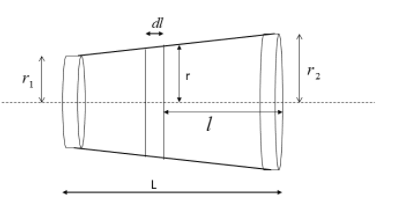
From the above figure, the radius $r$ can be calculated as given by,
$r = {r_1} + \dfrac{{\left( {{r_2} - {r_1}} \right)l}}{L}$
Where $l$ -length from one end of the wire at the radius $r$
$L$ - the total length of the wire before elongation
The force acting on both sides is equal but opposite in direction. The elongation of the wire can be calculated at the point radius $r$
From young’s modulus formula,
$Y = \dfrac{{stress}}{{strain}}$
$stress = \dfrac{F}{A}$
Where $F$ - force applied
$A$ - cross sectional area of wire of radius r
$strain = \dfrac{{\Delta dl}}{{dl}}$
Where $\Delta dl$- change in length
$dl$- original length
Therefore young’s modulus becomes,
$Y = \dfrac{{\dfrac{F}{A}}}{{\dfrac{{\Delta dl}}{{dl}}}}$
$\Delta dl = \dfrac{{F.dl}}{{AY}}$
$\Delta dl = \dfrac{{F.dl}}{{\pi {r^2}Y}}$
Substituting the value of radius r in the above equation, we get
$\Delta dl = \dfrac{{F.dl}}{{\pi {{\left( {{r_1} + \dfrac{{\left( {{r_2} - {r_1}} \right)l}}{L}} \right)}^2}Y}}$
Integrating on both sides with limits from$0$to $L$, we get the net elongation is given by
$\int {\Delta dl} = \int\limits_0^L {\dfrac{{F.dl}}{{\pi {{\left( {{r_1} + \dfrac{{\left( {{r_2} - {r_1}} \right)l}}{L}} \right)}^2}Y}}}$
Net elongation$= \dfrac{F}{{Y\pi }}\left[ {\dfrac{{ - 1}}{{\left( {{r_1} + \dfrac{{\left( {{r_2} - {r_1}} \right)l}}{L}} \right)\left( {\dfrac{{{r_2} - {r_1}}}{L}} \right)}}} \right]_0^L$
$= \dfrac{1}{{\left( {\dfrac{{{r_2} - {r_1}}}{L}} \right)}} \times \dfrac{F}{{Y\pi }} \times \left( { - \dfrac{1}{{{r_2}}} + \dfrac{1}{{{r_1}}}} \right)$
$= \dfrac{{FL}}{{\left( {{r_2} - {r_1}} \right) \times Y\pi }} \times \dfrac{{\left( {{r_2} - {r_1}} \right)}}{{{r_1}.{r_2}}}$
Net elongation$= \dfrac{{FL}}{{{r_1}{r_2}Y\pi }}$
From the above derivation, the elongation of the wire $= \dfrac{{FL}}{{{r_1}{r_2}Y\pi }}$

Note: The elongation means the material length is to be increased when it is subjected to tensile force acted axially in the material. The elongation of any material depends on the same material properties like density, ductility, etc., and the most important is the tensile force acting on the material. The elongation of material under stress is calculated in the percentage of elongation.