Question
Question: A slab of thickness 1.5cm and refractive index 1.5 is introduced between the image and the lens. Fin...
A slab of thickness 1.5cm and refractive index 1.5 is introduced between the image and the lens. Find the new position of the object so that the image is again formed on the screen.
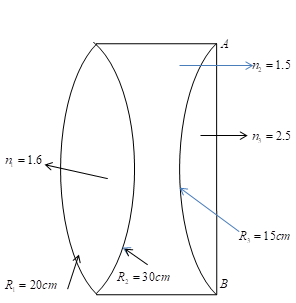
Solution
When the slab is introduced between the image and the object here there is a shift in the image away from the slab. It is a case like three mediums with different refractive index are placed together thus we will calculate the equivalent focal length of the combined lens then after getting the focal length and new image position we will use lens formula to get the new position of the object.
Formula used-
feq1=f11+f21+f31
Where
feq is the equivalent focal length of the lens
f1,f2,f3 is the focal length of the three materials of the lens.
Δx=(1−n1)t
Δx is the shift in the image from the slab due to introduction of slab.
n is the refractive index of the slab
t is the thickness of the slab
f1=(n−1)(R11−R21)
Where
f is the focal length
n is the refractive index
R1,R2 is the radius of curvature
Complete step-by-step answer:
Given
Thickness of the slab = 1.5cm
Refractive index of the slab = 1.5
Now we will find the focal length of each lens using the formula
f1=(n−1)(R11−R21)
Focal length of first lens and substituting the values as given in the figure
f11=(n−1)(R11−R21) f11=(1.6−1)(201−−301)=201cm−1
Focal length of second lens and substituting the values as given in the figure
f21=(n−1)(R21−R31) f21=(1.5−1)(−301−151)=201cm−1
Focal length of third lens and substituting the values as given in the figure
f31=(n−1)(R21−R31) f31=(2.5−1)(151−∞1)=101cm−1
The equivalent focal length is given by
feq1=f11+f21+f31
Substituting the values of the focal length calculated above in the equivalent focal length formula.
feq1=201−201+101 feq1=101 feq=10cm
Therefore, the image formed on the screen will be 10cm away from the lens, and the object is at infinity
The shift in the image due to introduction of the slab between them is given by
Δx=(1−n1)t
Substituting the value in the above equation from the data given in the question
Δx=(1−1.51)×1.5 Δx=0.5
Therefore due to shifting, the image position is
v=10−0.5=9.5
The distance of the object so that the image will formed on the screen is given by
f1=v1−u1
Substituting the value of the equivalent focal length, image distance
101=9.51−u1 u1=101−9.51 u=190cm
Therefore the object distance is 190cm.
Note: In order to solve these types of questions, you need to learn all the formulas and the concept behind each formula. In the above question, we proceed first by calculating the focal length of the combined lens and then calculated the shift in the image and at last using lens formula, we calculated the object distance so that due to introduction of slab the image will again formed on the screen.
