Question

A slab of refractive index $\mu$ is placed in air and light is incident at maximum angle $\theta_{o}$ from vertical. Find a minimum value of $\mu$ for which total internal reflection takes place at the vertical surface.

Answer 1

A ray of light runs from a medium to that of air. Light ray will be refracted at the interface dividing the two media. Since it moves from a medium of a more extensive refractive index to a more moderate refractive index, the refracted light ray turns away from the normal. At a particular angle of incidence, the ray of an incident of light is refracted to pass along the water's surface. This unique angle of incidence is named the critical angle. Here the refraction angle is $90$ degrees. When the incidence angle is higher than the critical angle, the incident ray has reflected the medium.

Complete step-by-step solution:
First, we will use Snell’s law at the interface.
$\mu sin r = sin \theta_{o}$……(1)

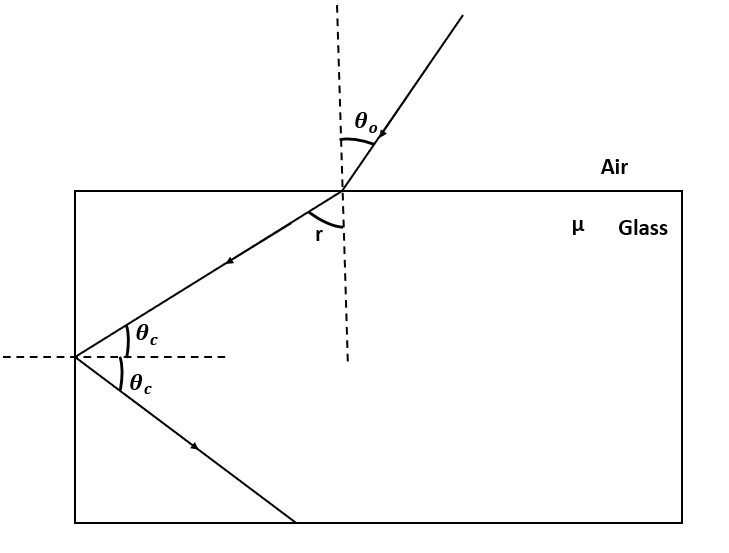
Now, we will see the total internal reflection at the vertical boundary.
$\mu sin \theta_{c} = sin 90^{\circ} = 1$
As we know, $\theta_{c} + r = 90^{\circ}$
Put $\theta_{c} = 90^{\circ} - r$
$\mu sin (90^{\circ} – r) = 1$
Now, we get
$\mu cos r = 1$……(2)
Squaring and adding equations ($1$) and ($2$).
$\mu^{2} \left( sin^{2}r + cos^{2}r \right) = sin^{2} \theta_{o} + 1$
Put $sin^{2}r + cos^{2}r = 1$, we get,
$\mu^{2} = sin^{2} \theta_{o} + 1$
This gives,
$\mu = \sqrt{ sin^{2} \theta_{o} + 1}$

Note: Total internal reflection states that the phenomenon occurs when the light rays move from a higher optically denser medium to a small optically denser medium. The two requirements of total internal reflection: - The light ray travels from a more dense medium to a slightly dense medium, and the incidence angle must be larger than the angle of critical.