Question

A slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor but has the thickness $\dfrac{d}{2}$, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor.

Answer 1

We will use the basic formula which is used for the capacitance with only air between the plates of the capacitor. After filling up some space by dielectric the formula changes as the distance changes. For this there must be the subtraction of original thickness from the new one which is obtained as $\dfrac{1}{k}$ times the original one.

Formula used: $C=\varepsilon \left( \dfrac{A}{d} \right)$ where C is capacitance, A is area, d is distance of separation between the plates in a capacitor and $\varepsilon$ is called electrostatic constant.

Complete step by step answer:
Capacitance: It is a property of any kind of an electric conductor. This means the amount of some electrical change that is stored per unit charged of an electric potential.
Parallel plate capacitance: As the name suggests, this type of a capacitance is generally of a parallel plate structure. It is mostly used in electronic circuits for tuning. The formula of parallel plate capacitor is $C=\varepsilon \left( \dfrac{A}{d} \right)$ where C is capacitance, A is area, d is distance of separation between the plates in a capacitor and $\varepsilon$ is called electrostatic constant.
According to the description of the slab in the question the figure to be drawn is shown below.

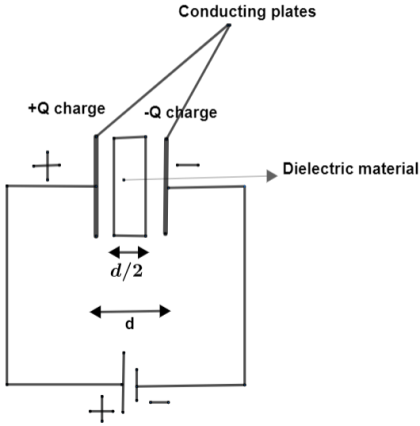
Distance between the two slabs of the capacitor is d and the thickness of the dielectric slab is $\dfrac{d}{2}$. Now, we will find capacitance after the addition of dielectric in between capacitor plates. This can be done by formula $C=\varepsilon \left( \dfrac{A}{d-t+\dfrac{t}{k}} \right)$ this is because of the presence of the electric field as $\dfrac{1}{k}$ times the outside field. So,
$\begin{aligned} & C=\varepsilon \left( \dfrac{A}{d-t+\dfrac{t}{k}} \right) \\\ & \Rightarrow C=\varepsilon \left( \dfrac{A}{d-t\left( 1-\dfrac{1}{k} \right)} \right) \\\ & \Rightarrow C=\varepsilon \left( \dfrac{A}{d-\left( \dfrac{d}{2} \right)\left( 1-\dfrac{1}{k} \right)} \right) \\\ \end{aligned}$
This further results into,
$\begin{aligned} & \Rightarrow C=\dfrac{\varepsilon }{\dfrac{d}{2}}\left( \dfrac{A}{2-\left( 1-\dfrac{1}{k} \right)} \right) \\\ & \Rightarrow C=\dfrac{\varepsilon }{\dfrac{d}{2}}\left( \dfrac{A}{2-1+\dfrac{1}{k}} \right) \\\ & \Rightarrow C=\dfrac{\varepsilon }{\dfrac{d}{2}}\left( \dfrac{A}{1+\dfrac{1}{k}} \right) \\\ & \Rightarrow C=\dfrac{2\varepsilon }{d}\left( \dfrac{kA}{k+1} \right) \\\ \end{aligned}$

Hence the required value of capacitance with dielectric in between its plates is $C=\dfrac{2\varepsilon }{d}\left( \dfrac{kA}{k+1} \right)$.

Note: To solve this question one should know the following points:
(1) The definition of capacitance and the formula $C=\varepsilon \left( \dfrac{A}{d} \right)$ is taken when there is just air in between the plates.
(2) As soon as the dielectric slab enters the space, so we will apply the formula $C=\varepsilon \left( \dfrac{A}{d-t+\dfrac{t}{k}} \right)$ for finding capacitance.