Question

A slab of copper of thickness $\dfrac{d}{2}$ is introduced between the plates of a parallel plate capacitor where $d$ is the separation between the two plates. If the capacitance of the capacitor without the copper slab is $C$ and with the slab is $C$’ then find $\dfrac{{C'}}{C}$ .
A. $\sqrt 2$
B. $2$
C. $1$
D. $\dfrac{1}{{\sqrt 2 }}$

Answer 1

The capacitance of a capacitor changes if the area of cross-section of the plates changes or if the separation between the plates varies. We find the capacitance to be inversely proportional to the distance of separation and directly proportional to the area of the plates. When the copper slab is inserted between the plates, the separation between the capacitor plates decreases.

Formula used:
->The capacitance of a capacitor with air as the medium between the plates is given by, $C = \dfrac{{A{\varepsilon _0}}}{d}$ where $A$ is the area of cross-section of the plates, $d$ is the distance of separation between the plates and ${\varepsilon _0}$ is the permittivity of free space.
->The capacitance of a capacitor with a material of thickness $t$ as the medium between the plates is given by, $C' = \dfrac{{A{\varepsilon _0}}}{{d - t}}$ where $A$ is the area of cross-section of the plates, $d$ is the distance of separation between the plates and ${\varepsilon _0}$ is the permittivity of free space.

Complete step-by-step solution:
->Step 1: Sketch a figure representing the capacitor before and after the copper slab is introduced.

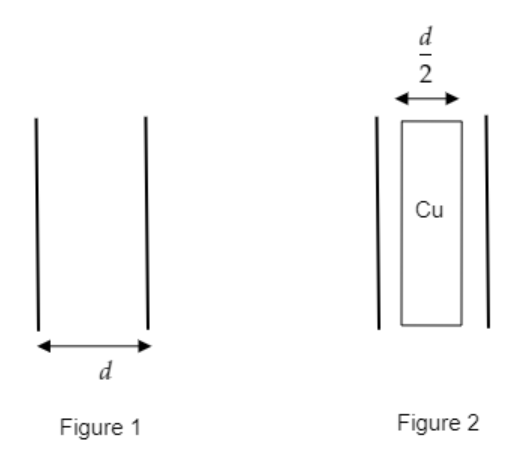
In figure 1, the medium between the plates is air and the separation between the plates is $d$ .
In figure 2, the medium between the plates becomes the copper slab of thickness $t = \dfrac{d}{2}$ .
Then the separation between the plates will be $d - t = d - \dfrac{d}{2}$ .
Given, the capacitor before inserting the copper slab is $C$ and after inserting the slab it is $C$’.
->Step 2: Express the capacitance of the capacitor before and after the insertion of the slab to obtain $\dfrac{{C'}}{C}$ .
The capacitance of the capacitor before inserting the copper slab is given by, $C = \dfrac{{A{\varepsilon _0}}}{d}$ ------- (1)
The capacitance of the capacitor after inserting the copper slab is given by,
$C' = \dfrac{{A{\varepsilon _0}}}{{\left( {d - \dfrac{d}{2}} \right)}} = \dfrac{{2A{\varepsilon _0}}}{d}$ ------- (2)
Then dividing equation (2) by (1) we get, $\dfrac{{C'}}{C} = \dfrac{{\left( {\dfrac{{2A{\varepsilon _0}}}{d}} \right)}}{{\left( {\dfrac{{A{\varepsilon _0}}}{d}} \right)}} = 2$
Thus the ratio of the capacitances after and before the insertion of the copper slab is $\dfrac{{C'}}{C} = 2$ .
So the correct option is B.

Note:-
The introduction of the copper slab only changed the separation between the plates. It has no effect on the area of cross-section of the plates. As the capacitance is inversely proportional to the separation between the plates, the new capacitance can be predicted to be twice that of its original value since the insertion of the copper slab caused the distance of separation between the plates to become half of its initial separation.