Question
Question: A skier plans to ski a smoothly fixed hemisphere of the radius \(R\). He starts from rest from a cur...
A skier plans to ski a smoothly fixed hemisphere of the radius R. He starts from rest from a curved smooth surface of height 4R. The angle θ at which he leaves the hemisphere is:
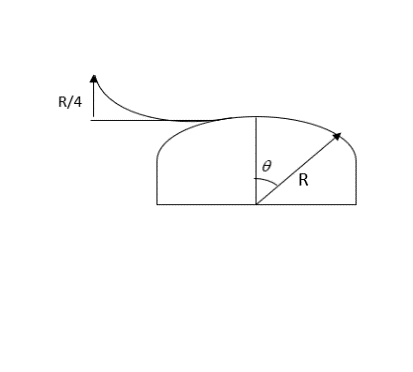
(A)cos−1(32)
(B)cos−1(35)
(C)cos−1(65)
(D)cos−1(235)
Solution
Here the skier skies in a hemisphere radius are given. Its height from the smooth surface is given. At an angle, θ the skier leaves the hemisphere. Now using the given data draw a free body diagram. The force on a body is a centripetal force because the body undergoes circular motion. Equate the vertical and horizontal component of force with centripetal force and apply it to the work-energy theorem equation.
Formula used:
F=Rmv2
Where F s the centripetal force, v is the velocity, R is the radius of the hemisphere.
(KE)f−(KE)i=work
Where (KE)f,(KE)i are the final and initial kinetic energy respectively
Complete step by step answer:
Free body diagrams will consist of a simplified version of the body. straight arrows are used for the force to point the direction they act on the body. The Moments are shown as curved arrows pointing in the direction they act on the body and they have a coordinate system.
The number of forces in a free body diagram depends on the problem and the assumptions made, common assumptions are neglecting air resistance and friction and assuming rigid bodies. All forces must balance to zero.
A force that makes a body move in a curved path is called centripetal force.
The vertical height is 4R+R(1−cosθ)
Free body diagram is given below
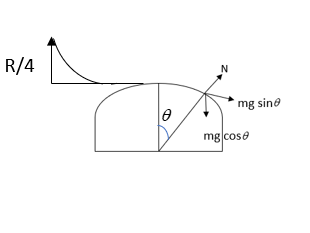
mgcosθ−N=Rmv2
At the time when the skier leaves the hemisphere, the value of N=0
⇒gcosθ=Rv2
⇒(KE)f−(KE)i=mg[4R+R(1−cosθ)]
⇒21mv2=mg[4R+R(1−cosθ)]
⇒21mv2=mg[4R+R(1−cosθ)]
⇒23cosθ=45
⇒cosθ=65
Hence option (C) is the right option.
Note: If the body is moving then resultant forces and moments can be non-zero. A force that makes a body move in a curved path is called centripetal force. Centripetal force is directed towards the center and it acts on a body executing circular motion. In the Free body, diagram force is shown as straight-arrow pointing at the direction where force at.
