Question

A sitting cat in a field suddenly sees a standing dog. To save its life the cat runs away in a straight line with a constant velocity $u$ , in a direction perpendicular to the direction of the line joining the cat and the dog. At the same time the dog also starts running with the same speed $u$ towards the cat such that the dog always heads the cat. If initial separation between them is $d$ then minimum separation between them is
\left( A \right)\dfrac{d}{{\sqrt 3 }} \\\ \left( B \right)\dfrac{d}{{\sqrt 2 }} \\\ \left( C \right)\dfrac{d}{{\sqrt 4 }} \\\ \left( D \right)Zero \\\

Answer 1

Hint : We are first going to analyze the situation and represent it using the vectors in a diagram. Therein, the distance of the least approach is also shown which is calculated later on using the information given and depending on the angle between the net velocity vector and the velocity of the dog.

Complete Step By Step Answer:
According to the situation as given in the question,
Velocity of the cat in the perpendicular direction to the line joining them is $u$
And that of the dog in the cat’s direction, $u$
Minimum separation between them is $d$
If we draw a figure corresponding to this situation,

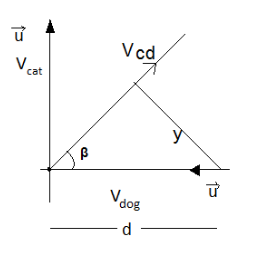
Here, in this figure, ${V_{cd}}$ is the velocity of the cat with respect to the dog which can be calculated as:
${\vec V_{cd}} = {\vec V_{cat}} - {\vec V_{dog}}$
Now, the tangent of the angle $\beta$ can be calculated as
$\tan \beta = \dfrac{{{{\vec V}_{cat}}}}{{{{\vec V}_{dog}}}}$
Now, if the distance of the closest approach is $y$ , then the relation for it is given by
$\sin \beta = \dfrac{y}{d}$
Thus, we can calculate $y$ as:
$y = d\sin \beta = \dfrac{{d\tan \beta }}{{\sqrt {1 + {{\tan }^2}\beta } }}$
Now putting the values, we get
y = \dfrac{{d{{\vec V}_{cat}}}}{{\sqrt {{{\vec V}^2}_{cat} + {{\vec V}^2}_{dog}} }} \\\ \Rightarrow y = \dfrac{{du}}{{\sqrt {{u^2} + {u^2}} }} = \dfrac{d}{{\sqrt 2 }} \\\
Hence, the option $\left( B \right)\dfrac{d}{{\sqrt 2 }}$ is the correct answer.

Note :
It is important to note that the relative velocity of the cat with respect to the dog cannot be found by simple addition or subtraction as they are not moving in the same directions. The paths across which both of them are and the angles which they make is considered. Hence the vector calculations are taken.