Question
Question: A siphon tube is discharging a liquid of specific gravity 0.9 from a reservoir as shown in the figur...
A siphon tube is discharging a liquid of specific gravity 0.9 from a reservoir as shown in the figure to find the pressure at the highest point B.
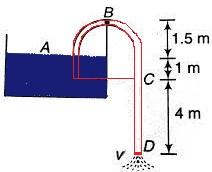
Solution
Here we have to use Bernoulli's equation; the equation is based upon the principle of conservation of energy. It states that the total energy that is related with a flowing fluid remains constant. The energy related with the flowing fluid is potential energy, kinetic energy and pressure. Here to find out the pressure at the highest point B one has to equate pressure at point A to pressure at point B.
Formula used:
P+21ρv2+ρgh=constant ;
P = Pressure;
ρ= Relative density or specific gravity (0.9);
g = Gravitational Constant;
h = Height;
v = Velocity.
Complete step by step solution:
Equate the Bernoulli’s equation for two points A and D, Find v
PA+21ρv2+ρgh=PD;
Here PA and PD are atmospheric pressure which is 1.01×105Pa.
PA+21ρv2+ρgh=PD+21ρv2+ρgh;
Here PA and PD are equal, they will cancel out,
21ρv2+ρgh=21ρv2+ρgh;
Put the given values in the above equation
21ρv2+ρg×5=21ρv2+ρg×0;
At point A there will be no velocity in the liquid , v = 0;
ρg×5=21ρv2
Here the relative densities are equal as the liquid is same,
g×5=21v2;
Solve,
g×5×2=v2;
v=10g ;
v=9.8×10 ;
v=9.9 m/s ;
Now, equate the Bernoulli’s equation at point A and at point B,
PA+21ρv2+ρgh=PB+21ρv2+ρgh;
Put the values in the above equation,
PA+21ρ×0+ρg×0=PB+21ρv2+ρg(1⋅5);
Simplify the above equation,
PA+0+0=PB+21ρv2+ρg(1⋅5);
Here,PA=Po, Put value 1.01×105Pa.
1.01×105=PB+21×900×(9.9)2+900×9⋅8×1⋅5
Take PB to LHS and the rest to RHS and solve,
PB=1.01×105−21×900×(9.9)2−900×9⋅8×1⋅5;
Do the necessary calculation,
PB=4.36×104 Pa;
Pressure at the highest point B is PB=4.36×104 Pa.
Note: Here we have to first equate point A and D by using the Bernoulli’s equation and find out the velocity and after that to find out the pressure at the highest point B we have to equate the Bernoulli’s equation at point A and B.
