Question
Question: A siphon has a uniform circular base of diameter \(\dfrac{8}{\sqrt{\pi }}\) with its crest at 1.8m a...
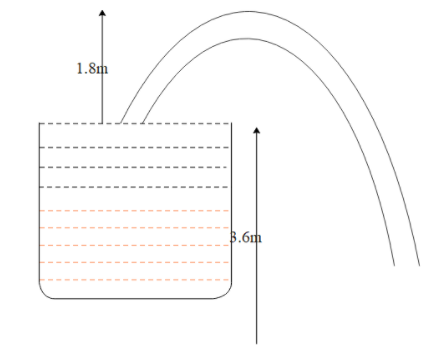
A siphon has a uniform circular base of diameter π8 with its crest at 1.8m above water level as in figure. Then,
A) velocity of flow is 62
B) discharge rate of flow is 9.6×10−3m3s−1
C) absolute pressure at crest level a is 4.6×104Nm−2
D) none
Solution
Find the velocity at a point by using Bernoulli's equation. The equation explains that the hey sum of pressure energy, kinetic energy and potential energy often incompressible non viscous fluid remains constant.
Formulas used:
P+ρgd+21ρv2=same
Complete answer:
Let us write down the given parameters,
the diameter of the base is given, radius will be,
r=2D=π4
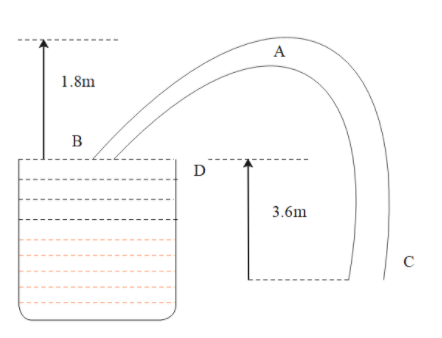
distance between points A and B is 1.8m. distance between point b and c will be 3.6m.
points a, b, c are assigned as shown in the diagram.
let us now apply the Bernoulli’s equation at top layer of water in water vessel and the end of the pipe, at point c,
PD+ρgyD+21ρvD2=PC+ρgyC+21ρvC2⇒PD=PC=P0vD=0,yD−yC=3.6m⇒P0+ρg(yD−yC)=P0+21ρvD2⇒vC=62ms−1
Therefore, option a is correct.
Discharge of water is
av=π×(π4)2×10−4×62⇒av=962×10−4m3s−1
Therefore, option b is correct.
Let us apply Bernoulli’s theorem at point a and c,
PA+ρgyA+21ρvA2=PC+ρgyC+21ρvC2⇒vA=vC,yA−yC=5.4m⇒PA=PC−ρg(yA−yC)⇒4.6×104Nm−2
Therefore, option c is also correct.
Hence, the correct options are a, b and c.
Additional information:
Bernoulli’s principle formulated by Daniel Bernoulli states that as the speed of a moving fluid increases, the pressure within the fluid decreases. The actual Bernoulli’s equation was derived in 1752. The total mechanical energy of the moving fluid comprising the gravitational potential energy of elevation, energy of the fluid pressure and kinetic energy remains constant according to this principle. The density of the incompressible fluid remains constant at both points and the energy of the fluid must be conserved as there are no viscous forces in the fluid. If these 2 conditions are satisfied, we can use the Bernoulli equation to solve the question. If the fluid is in streamline flow, compressible, we can say that mass of the fluid passing through different cross sections is equal. Equation of principle of continuity says that the product of density area and volume, the rate of mass entering is constant.
Note:
The liquid must be incompressible, and the density must be constant energy of the fluid is conserved as there will not be any viscous forces present. If in case the density changes r there's viscous forces present in the fluid, this principle cannot be used.
