Question

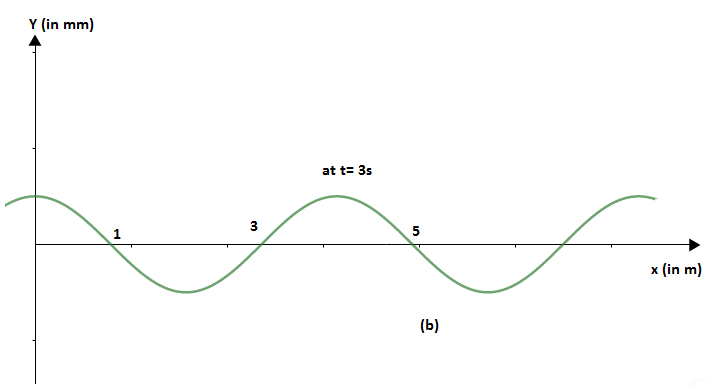
A sinusoidal wave propagates along a string. In figure (a) and (b). ‘y’ represents displacement of particles from the mean position. ‘x’ and ‘t’ have usual meanings. Find: maximum velocity and maximum acceleration of the particles.

$\begin{aligned} & A.\dfrac{3\pi }{2}mm/s,\dfrac{3{{\pi }^{2}}}{4}mm/{{s}^{2}} \\\ & B.\dfrac{5\pi }{2}mm/s,\dfrac{5{{\pi }^{2}}}{4}mm/{{s}^{2}} \\\ & C.\dfrac{7\pi }{2}mm/s,\dfrac{3{{\pi }^{2}}}{4}mm/{{s}^{2}} \\\ & D.\dfrac{2\pi }{3}mm/s,\dfrac{3{{\pi }^{2}}}{4}mm/{{s}^{2}} \\\ \end{aligned}$

Answer 1

Velocity is defined as the rate of change of displacement of a particle. And the acceleration of a particle is the rate of change of velocity of that particle. Calculate angular acceleration ‘w’ and maximum amplitude ‘A’ using their mathematical expressions. Then find out the values of maximum velocity and maximum acceleration of particles by deducing the linear equivalent of these rotational quantities i.e. angular acceleration and angular velocity.
Formula used:
$\begin{aligned} & \omega =\dfrac{2\pi }{T} \\\ & {{v}_{\max }}=\omega A \\\ & {{a}_{\max }}={{\omega }^{2}}A \\\ \end{aligned}$

Complete answer:
We must study the given figures carefully first. After careful consideration we can notice that from both figures (a) and (b) the values of t = 4sec. Now, we need to find the value of angular acceleration. Using the mathematical expression for angular velocity we have:
$\omega =\dfrac{2\pi }{T}=\dfrac{2\pi }{4}=\dfrac{\pi }{2}rad/\sec$
Amplitude is A= 3mm
Let’s find out the maximum velocity and acceleration of the particle we know that ${{v}_{\max }}=\omega A$
Where, ‘ω’ represents the angular velocity and ‘A’ represents the amplitude
${{v}_{\max }}=\dfrac{\pi }{2}\times 3=\dfrac{3\pi }{2}mm{{s}^{-1}}$
Now acceleration of the particle can be found by using the following formula.
$\begin{aligned} & {{a}_{\max }}={{\omega }^{2}}A \\\ & {{a}_{\max }}={{\left( \dfrac{\pi }{2} \right)}^{2}}\times 3={{\dfrac{\pi }{4}}^{2}}\times 3 \\\ & {{a}_{\max }}=\dfrac{3{{\pi }^{2}}}{4}mm{{s}^{-2}} \\\ \end{aligned}$
Therefore, maximum velocity and maximum acceleration of the particles are$\dfrac{3\pi }{2}mm/s,\dfrac{3{{\pi }^{2}}}{4}mm/{{s}^{2}}$.

So, the correct answer is “Option A”.

Note:
It is advised to clearly understand the figures given in the question and then solve the further question. We need to remember the units of ω that are rad/sec. Additionally, notice how the angular velocity and angular acceleration are related to their linear quantities. These are useful expressions. Similarly, every rotational quantity can be converted into its linear equivalent by multiplying it with its proportionality constant with the linear quantity.