Question
Question: A Single wire \[ABC\] passes through a ring \(C\) which revolves a constant speed in the horizontal ...
A Single wire ABC passes through a ring C which revolves a constant speed in the horizontal circle of radius r as shown in the figure. The speed of revolution is.
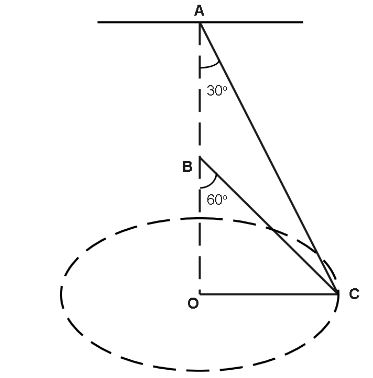
Solution
To solve this question first one must have a concept of Newton’s law of motion. Here we first draw the diagram where we have resolved all the forces and the solved to obtain the equation and the solved for centripetal force and the equated both the equation to get our required solution.
Formula used:
Fc=rmv2
Where, Fc is the centripetal force, m is the mass, r is the radius and v is the velocity.
Complete step by step answer:
Let us draw the all the forces of acting on the diagram of the given figure,
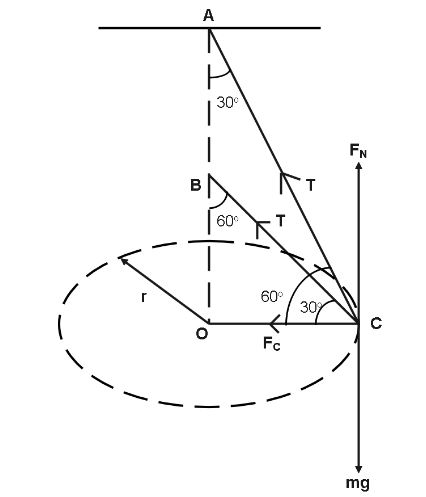
From the figure we can say that,
FN=Mg
And we can write the above equation as,
Tsin30∘+Tsin60∘=mg ⇒2T+23T=mg
And on further simplifying we can write,
⇒2T+23T=mg
⇒(3+1)2T=mg -----(1)
And we know that centripetal force is given by,
Fc=rmv2
So, we can write as,
