Question
Question: A single slit of width b is illuminated by a coherent monochromatic light of wavelength \(\lambda\)....
A single slit of width b is illuminated by a coherent monochromatic light of wavelength λ. If the second and fourth minimum in the diffraction pattern at a distance 1m from the slit are 3 cm and 6 cm respectively from the central maximum, what is the width of the central maximum? (i.e. distance between first minimum on either side)
A. 4.5 cm
B. 6.0 cm
C. 1.5 cm
D. 3.0 cm
Solution
Hint: We need to know the condition for the minimum in a single slit diffraction experiment. Then using only one of the two given data we can find the answer. We also need to use basic approximations with sine and tangent functions.
Formula used: b.sinθ=mλ
Complete step-by-step solution:
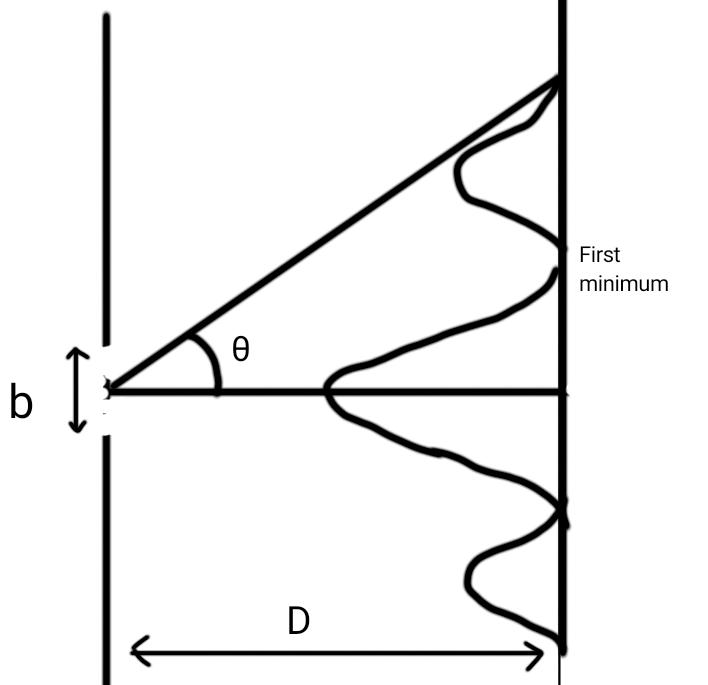
When light passes through a very thin slit whose dimension is comparable to the wavelength of light, it gets diffracted. It means if you place a screen before such a slit, you will see alternate dark and bright patterns.
The condition for diffraction minimum in single slit diffraction experiment is given as,
b.sinθ=mλ
Where, θ is called angle of diffraction. λ is the wavelength of light and ‘m’ is the order of the minimum.
We will take sinθ=tanθ in the whole calculation.
For second diffraction minimum,
b.sinθ2=2.λ
⇒sinθ2=b2λ
Now, if the distance between screen and slit is D=1m=100cm (given) and if the distance of m-th minimum from the central band is xm , we can write,
sinθ2=tanθ2=Dx2=100cm3cm
So, we have,
b2λ=100cm3cm
bλ=2003
Now, for the first minimum,
b.sinθ1=1.λ
tanθ1=sinθ1=bλ
Distance of first minimum from central maximum in one direction is,
xc=D.tanθ1=bD.λ
Now, length of central maximum, l=2xc.
l=b2Dλ=2×100×2003=3cm
Hence option D is the correct answer.
Additional information:
The distance between two successive dark patterns decreases as their distance is increased from central maximum. Again, the central band is the brightest. This makes it different from interference of light, which is another phenomenon.
Note: In this problem, remember the following things,
1. One can use data related to the fourth minimum as well. The answer would be the same.
2. While putting different values on an equation, remember to keep them in the same unit system.
3. We can equal sinθ and tanθ only when θ is very small.
