Solveeit Logo
Login

Question

Question: A single circular loop of wire with radius 0.02 m carries a current of 8.0 A. It is placed at the ce...

A single circular loop of wire with radius 0.02 m carries a current of 8.0 A. It is placed at the centre of a long solenoid that has length 0.65m, radius 0.080 m and 1300 turns. (Axis of circular loop coincide with axis of solenoid). Let 'i' be the current in solenoid.

A

If i=100 mA, the magnetic field at the center of coil can be zero.

B

If i = 44 mA, the magnetic field at the center of coil can be zero.

C

If i = 100 mA, the magnetic field at the center of coil can be 8π×10−5\pi \times 10^{-5} T.

D

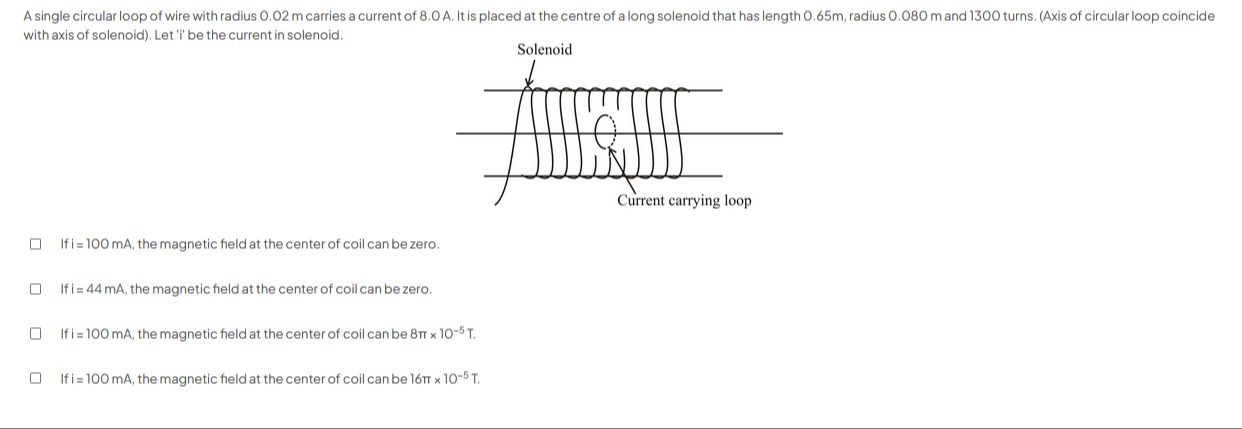
If i = 100 mA, the magnetic field at the center of coil can be 16π×10−5\pi \times 10^{-5} T.

Answer

If i=100 mA, the magnetic field at the center of coil can be zero. If i = 100 mA, the magnetic field at the center of coil can be 16π×10−5\pi \times 10^{-5} T.

Explanation

Solution

The magnetic field at the center of the circular loop of radius Rc=0.02R_c = 0.02 m carrying current Ic=8.0I_c = 8.0 A is given by Bc=μ0Ic2RcB_c = \frac{\mu_0 I_c}{2 R_c}.

Bc=4π×10−7 T m/A×8.0 A2×0.02 m=32π×10−70.04 T=800π×10−7 T=8π×10−5 TB_c = \frac{4\pi \times 10^{-7} \text{ T m/A} \times 8.0 \text{ A}}{2 \times 0.02 \text{ m}} = \frac{32\pi \times 10^{-7}}{0.04} \text{ T} = 800\pi \times 10^{-7} \text{ T} = 8\pi \times 10^{-5} \text{ T}.

The number of turns per unit length of the solenoid is n=NL=13000.65 m=2000 turns/mn = \frac{N}{L} = \frac{1300}{0.65 \text{ m}} = 2000 \text{ turns/m}.

The magnetic field inside a long solenoid, at its center, is given by Bs=μ0niB_s = \mu_0 n i, where ii is the current in the solenoid.

Bs=(4π×10−7 T m/A)×(2000 m−1)×i=8π×10−4i T/AB_s = (4\pi \times 10^{-7} \text{ T m/A}) \times (2000 \text{ m}^{-1}) \times i = 8\pi \times 10^{-4} i \text{ T/A}.

The circular loop is placed at the center of the solenoid with coincident axes. The magnetic field due to the loop and the solenoid at the center are along the common axis. The total magnetic field at the center is the vector sum of the two fields. The direction of the field due to the loop is fixed by the direction of IcI_c. The direction of the field due to the solenoid depends on the direction of ii. The two fields can be in the same direction or opposite directions. The magnitude of the total magnetic field is ∣Bc±Bs∣|B_c \pm B_s|.

Let's evaluate the given statements:

  • Statement 1: If i=100i = 100 mA, the magnetic field at the center of coil can be zero. i=100i = 100 mA =0.1= 0.1 A. Bs=8π×10−4 T/A×0.1 A=8π×10−5B_s = 8\pi \times 10^{-4} \text{ T/A} \times 0.1 \text{ A} = 8\pi \times 10^{-5} T. Bc=8π×10−5B_c = 8\pi \times 10^{-5} T. If the currents are directed such that the magnetic fields are in opposite directions, the total magnetic field magnitude is ∣Bc−Bs∣=∣8π×10−5−8π×10−5∣=0|B_c - B_s| = |8\pi \times 10^{-5} - 8\pi \times 10^{-5}| = 0. So, the magnetic field at the center can be zero. Statement 1 is true.

  • Statement 2: If i=44i = 44 mA, the magnetic field at the center of coil can be zero. i=44i = 44 mA =0.044= 0.044 A. Bs=8π×10−4 T/A×0.044 A=3.52π×10−5B_s = 8\pi \times 10^{-4} \text{ T/A} \times 0.044 \text{ A} = 3.52\pi \times 10^{-5} T. Bc=8π×10−5B_c = 8\pi \times 10^{-5} T. For the total field to be zero, we need Bs=BcB_s = B_c. Since 3.52π×10−5≠8π×10−53.52\pi \times 10^{-5} \neq 8\pi \times 10^{-5}, the magnetic field at the center cannot be zero. Statement 2 is false.

  • Statement 3: If i=100i = 100 mA, the magnetic field at the center of coil can be 8π×10−58\pi \times 10^{-5} T. As calculated in Statement 1, when i=100i = 100 mA, Bs=8π×10−5B_s = 8\pi \times 10^{-5} T and Bc=8π×10−5B_c = 8\pi \times 10^{-5} T. The possible magnitudes of the total magnetic field are ∣Bc±Bs∣=∣8π×10−5±8π×10−5∣|B_c \pm B_s| = |8\pi \times 10^{-5} \pm 8\pi \times 10^{-5}|. This gives possible magnitudes 00 (when fields are opposite) and 16π×10−516\pi \times 10^{-5} T (when fields are in the same direction). The value 8π×10−58\pi \times 10^{-5} T is not a possible magnitude for the total field. Statement 3 is false.

  • Statement 4: If i=100i = 100 mA, the magnetic field at the center of coil can be 16π×10−516\pi \times 10^{-5} T. As calculated in Statement 3, when i=100i = 100 mA, Bs=8π×10−5B_s = 8\pi \times 10^{-5} T and Bc=8π×10−5B_c = 8\pi \times 10^{-5} T. If the currents are directed such that the magnetic fields are in the same direction, the total magnetic field magnitude is Bc+Bs=8π×10−5+8π×10−5=16π×10−5B_c + B_s = 8\pi \times 10^{-5} + 8\pi \times 10^{-5} = 16\pi \times 10^{-5} T. So, the magnetic field at the center can be 16π×10−516\pi \times 10^{-5} T. Statement 4 is true.

The correct statements are 1 and 4.