Question

A simple U shaped tube contains mercury in both its arms and to the same level. When water is poured to a height of 13.6 cm in one arm, the rise in the mercury level in the other is $x{\text{ cm}}$. Find the value of $x$. (Take the density of mercury as $13.6 \times {10^3}{\text{kg/}}{{\text{m}}^3}$ and the density of water as ${10^3}{\text{kg/}}{{\text{m}}^3}$ )
A) 13.6 cm
B) 10 cm
C) 1 cm
D) 1.36 cm

Answer 1

The pressure difference in the two arms of the tube when water is poured into one of its arms will be the same. The pressure is found to be proportional to the height of the liquid and its density.

Formula Used:
The pressure of a liquid at height $h$ is given by, $P = \rho gh$ where $\rho$ is the density of the liquid and $g$ is the acceleration due to gravity.

Complete step by step answer:
Step 1: Sketch the setup given in the question.

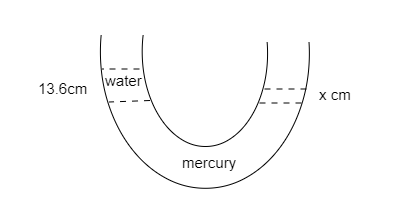
Step 2: List the known parameters of the problem.
Water is poured into one arm to a height of $h = 13.6{\text{cm}}$ .
The corresponding rise in the level of mercury in the other arm is unknown i.e., $x{\text{ cm}}$ .
The density of water is ${\rho _w} = {10^3}{\text{kg/}}{{\text{m}}^3}$ and the density of mercury is ${\rho _m} = 13.6 \times {10^3}{\text{kg/}}{{\text{m}}^3}$ .
Step 3: Find the pressure of water at a height of 13.6 cm.
The pressure of a liquid at height $h$ is given by, $P = \rho gh$ ------------ (1) where $\rho$ is the density of the liquid and $g$ is the acceleration due to gravity.
Let ${P_w}$ be the pressure of water. Then using equation (1) we express, ${P_w} = {\rho _w}gh$ ------- (2)
Substituting for ${\rho _w} = {10^3}{\text{kg/}}{{\text{m}}^3}$, $h = 13.6{\text{cm}}$ in equation (2) we get,
${P_w} = {10^3} \times g \times 0.136$ ------- (3)
Equation (3) gives the pressure of water at a height of 13.6 cm.
Step 4: Find the pressure of mercury at a height of $x{\text{ cm}}$.
The pressure of a liquid at height $h$ is given by, $P = \rho gh$ ------------ (1) where $\rho$ is the density of the liquid and $g$ is the acceleration due to gravity.
Let ${P_m}$ be the pressure of mercury. Then using equation (1) we express, ${P_m} = {\rho _m}gx$ ------- (4)
Substituting for ${\rho _m} = 13.6 \times {10^3}{\text{kg/}}{{\text{m}}^3}$ in equation (2) we get, ${P_m} = 13.6 \times {10^3} \times g \times x$ -------(5)
Equation (5) gives the pressure of mercury at a height of $x{\text{ cm}}$.
Step 5: Find the rise in the mercury level.
Since the two ends of the tube are open to the air above it and as the liquids filled in it are at rest, the pressure of water poured to a height of 13.6 cm in one arm will be equal to the pressure of mercury at a height $x{\text{ cm}}$ from its initial level in the other arm.
So, we have ${P_w} = {P_m}$ ------ (6)
Substituting equations (3) and (5) in equation (6) we get, ${10^3} \times 9.8 \times 0.136 = 13.6 \times {10^3} \times 9.8 \times x$
Solving for $x$ we get, $x = \dfrac{{{{10}^3} \times 0.136}}{{13.6 \times {{10}^3}}} = 0.01{\text{m}}$
$\therefore$ the rise in the level of mercury in the other arm is $x = 1{\text{cm}}$
The correct option is C.

Note: According to Pascal's principle, if the pressure in a liquid is changed at a particular point change is transmitted to the entire liquid without being diminished in magnitude, hence the rise in water level on one side increases the pressure, which needs to be compensated by the rise in mercury level in the other arm so that the liquid remains in equilibrium.