Question

A simple pendulum with bob of mass m and length x is held in position at an angle${\theta _1}$, and then angle ${\theta _2}$ with the vertical. When released from these positions, speeds with which it passes the lowest positions are ${v_1}$ and ${v_2}$ respectively. Then $\dfrac{{{v_1}}}{{{v_2}}}$ is
A. $\dfrac{{1 - \cos {\theta _1}}}{{1 - \cos {\theta _2}}}$
B. $\sqrt {\dfrac{{1 - \cos {\theta _1}}}{{1 - \cos {\theta _2}}}}$
C. $\sqrt {\dfrac{{2gx\left( {1 - \cos {\theta _1}} \right)}}{{1 - \cos {\theta _2}}}}$
D. $\sqrt {\dfrac{{1 - \cos {\theta _1}}}{{2gx\left( {1 - \cos {\theta _2}} \right)}}}$

Answer 1

Determine the vertical distance between the released position and lowest position of the pendulum. By the law of conservation of energy, the decrease in the potential energy of the pendulum is equal to the increase in its kinetic energy. Express the equation for law of conservation for both the cases and solve them to get the desired answer.

Formula used:
Kinetic energy, $K = \dfrac{1}{2}m{v^2}$,
where, m is the mass and v is the velocity.
Potential energy, $U = mgh$,
where, g is the acceleration due to gravity and h is the height.

Complete step by step answer:
Let the pendulum is held at angle $\theta$ with the vertical and then released. As the distance from the ground decreases, the potential energy of the pendulum also decreases. By the law of conservation of energy, we can say that the decrease in the potential energy of the pendulum is equal to the increase in its kinetic energy. Let us observe the following figure.

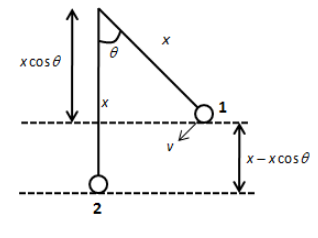
In the above figure, $\theta$ is the angle made by the pendulum with the vertical and x is the length of the pendulum.From position 1 to position 2, the distance covered by the pendulum is $x - x\cos \theta$.
Using the law of conservation of energy, we can write,
$mg\left( {x - x\cos \theta } \right) = \dfrac{1}{2}m{v^2}$
$\Rightarrow 2gx\left( {1 - \cos \theta } \right) = {v^2}$
$\Rightarrow \sqrt {2gx\left( {1 - \cos \theta } \right)} = v$

Let us express the above equation for angle ${\theta _1}$ and velocity ${v_1}$ as follows,
${v_1} = \sqrt {2gx\left( {1 - \cos {\theta _1}} \right)}$ …… (1)
Also, let us express the same for angle ${\theta _2}$ and velocity ${v_2}$ as follows,
${v_2} = \sqrt {2gx\left( {1 - \cos {\theta _2}} \right)}$ …… (2)
Dividing equation (1) and (2), we get,
$\dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{\sqrt {2gx\left( {1 - \cos {\theta _1}} \right)} }}{{\sqrt {2gx\left( {1 - \cos {\theta _2}} \right)} }}$
$\therefore \dfrac{{{v_1}}}{{{v_2}}} = \sqrt {\dfrac{{1 - \cos {\theta _1}}}{{1 - \cos {\theta _2}}}}$

So, the correct answer is option B.

Note: The crucial step in the solution is to find out the vertical distance covered by the pendulum from the position where it released. It is calculated by taking the cosine of the angle $\theta$. The lowest position of the pendulum is the mean position and at that position, the kinetic energy of the pendulum is the maximum. Note that the potential energy of the pendulum at lowest position may not be zero.