Question

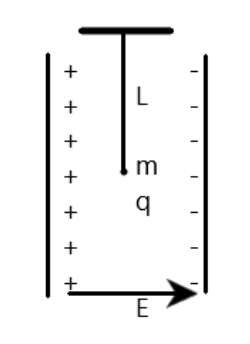
A simple pendulum of length $L$ is placed between the plates of a parallel plate capacitor having electric field $E$, as shown in figure. The bob has mass $m$ and charge $q$, the time period of the pendulum is given by

(A) $2\pi \sqrt {\dfrac{L}{{\sqrt {{g^2} + {{\left( {{a_e} = \dfrac{{qE}}{m}} \right)}^2}} }}}$
(B) $2\pi \sqrt {\dfrac{L}{{{g^2} + {{\left( {\dfrac{{qE}}{m}} \right)}^2}}}}$
(C) $2\pi \sqrt {\dfrac{L}{{{g^2} - {{\left( {\dfrac{{qE}}{m}} \right)}^2}}}}$
(D) $2\pi \sqrt {\dfrac{L}{{\sqrt {{g^2} - {{\left( {{a_e} = \dfrac{{qE}}{m}} \right)}^2}} }}}$

Answer 1

The weight (gravitational force) and the electric force are perpendicular to each other. Net force acting on the body should be used to calculate the net acceleration.
Formula used: In this solution we will be using the following formulae;
$T = 2\pi \sqrt {\dfrac{L}{{{a_r}}}}$ where $T$ is the period of oscillation of a simple pendulum, $L$ is the length of the pendulum, and ${a_r}$ is the resultant acceleration or net acceleration of the system.

Complete Step-by-Step Solution:
In the above, we see a pendulum placed between parallel plates capacitors. The bob has both a mass and a charge, we are to determine the period of oscillation of such a system.
Generally, the well known equation for the time period of a simple pendulum is given as
$T = 2\pi \sqrt {\dfrac{L}{g}}$ where $L$ is the length of the pendulum and $g$ is the acceleration due to gravity.
However, this equation is valid when no other forces are acting on the pendulum but the force of gravity (or weight) on the bob.
However, in our question above, the weight is not the only force acting on the bob, since the bob is charged and placed between a parallel plates capacitor.
Nonetheless, as obvious, the direction of the weight of a bob is perpendicular to the direction of the force of electric field (gravity acts downward while electric field acts rightwards), hence the net acceleration is given as
$a = \sqrt {{g^2} + {{\left( {\dfrac{{qE}}{m}} \right)}^2}}$
And the general equation, is given as
$T = 2\pi \sqrt {\dfrac{L}{{{a_r}}}}$ where $T$ is the period of oscillation of a simple pendulum, $L$ is the length of the pendulum, and ${a_r}$ is the resultant acceleration or net acceleration of the system.
Hence,
$T = 2\pi \sqrt {\dfrac{L}{{\sqrt {{g^2} + {{\left( {\dfrac{{qE}}{m}} \right)}^2}} }}}$

Hence, the correct option is A

Note: For clarity the resultant of the acceleration is given by $a = \sqrt {{g^2} + {{\left( {\dfrac{{qE}}{m}} \right)}^2}}$ because from principle of vectors, the magnitude of the resultant of two vectors which are perpendicular to each other can be given as the hypotenuse of the right angled triangle they may form.
Note that the acceleration of a charge in an electric field is given as
${a_e} = \dfrac{{qE}}{m}$ where $E$ is the electric field, $q$ is the charge and $m$ is the mass.