Question

A simple pendulum of length L and mass M is oscillating in a plane about a vertical line between angular limits $- \phi$ and $+ \phi$. For an angular displacement $\theta \left[ {\left| \theta \right| < \phi } \right]$, the tension in the string and the velocity of the bob are T and v respectively. The following relation holds well under the above conditions –
A. $T\cos \theta = Mg$
B. $T - Mg\cos \theta = \dfrac{{M{v^2}}}{L}$
C. Tangential acceleration = $g\sin \theta$
D. $T = Mg\cos \theta$

Answer 1

Draw the free body diagram of the forces acting on the bob and string of the pendulum. The forces acting on the bob are the weight of the bob and the centrifugal force. Use the Newton’s second law along the string to determine the net force along the string of the pendulum. The tangential acceleration of the pendulum is due to the force along the motion of the bob.

Formula used:
${F_c} = \dfrac{{M{v^2}}}{r}$
where, m is the mass, v is the velocity and r is the radius of circular motion.

Complete step by step answer:
To answer this question, we have to draw the free body diagram of the forces acting on the bob and string of the pendulum. The forces acting on the bob are the weight of the bob and the centrifugal force. The force in the string of the pendulum is the tension force which is the necessary force for the oscillation.

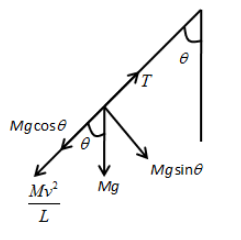
In the above figure, the net force in the direction of string is,
$T - Mg\cos \theta - \dfrac{{M{v^2}}}{l} = 0$
$\Rightarrow T - Mg\cos \theta = \dfrac{{M{v^2}}}{l}$
So, the option (B) is the correct answer.
Also, we can see in the above figure, the tangential acceleration responsible for the motion of the bob is due to the component of weight of the bob in the direction of motion. Therefore, we can write,
$mg\sin \theta = ma$
$\therefore a = g\sin \theta$
Therefore, the tangential acceleration of the bob is $g\sin \theta$.

So, the correct answer is option B and C.

Note: The direction of centrifugal force is away from the rigid support and not towards the rigid support. The force which goes towards the centre of circular motion is the centripetal force. The tension in the string is responsible for the radial acceleration while the component of the gravitational force is responsible for the tangential acceleration of the bob.