Question

A simple pendulum of length $l$ and bob mass $m$ is hanging in front of a large non-conducting sheet having surface charge density $\sigma$. If suddenly a charge $+ q$ is given to the bob and it is released from the position shown in figure. The maximum angle through which the string is deflected is $x{\tan ^{ - 1}}\left( {\dfrac{{\sigma q}}{{2{\varepsilon _0}mg}}} \right)$. Find $x$

Answer 1

To solve this question, we need to use the work energy theorem. For this we need to find out the total work done by the electrostatic and the gravitational forces on the bob. This work done has to be equated with the change in total kinetic energy of the bob.
Formula used: The formula used for solving this question is given by
$E = \dfrac{\sigma }{{2{\varepsilon _0}}}$, here $E$ is the electric field due to an infinite charged sheet having a surface charge density of $\sigma$.

Complete step-by-step solution:
Let the maximum deflection angle of the string be $\varphi$.
Since the sheet is negatively charged and the bob is given a positive charge, so the bob will be attracted towards the sheet. We know that the electric field due to a single large charged sheet at a point is given by
$E = \dfrac{\sigma }{{2{\varepsilon _0}}}$
Since the bob has a charge of $+ q$, so the electrostatic force on the bob is given by
${F_E} = qE$
$\Rightarrow {F_E} = \dfrac{{q\sigma }}{{2{\varepsilon _0}}}$...............(1)
Consider the bob at its maximum deflection position.

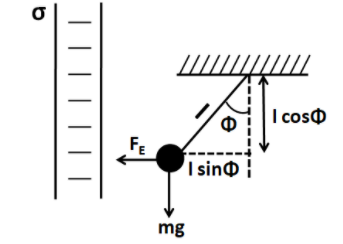
The horizontal displacement of the bob is given by
$x = l\sin \varphi$
Since the electrostatic force is towards the left, so the work done by the electrostatic force can be given by
${W_E} = {F_E}\left( {l\sin \varphi } \right)$
Putting (1) in the above equation, we have
${W_E} = \dfrac{{q\sigma }}{{2{\varepsilon _0}}}l\sin \varphi$................(2)
Also, the upward displacement of the bob is given by
$y = l - l\cos \varphi$
$\Rightarrow y = l\left( {1 - \cos \varphi } \right)$
Since the weight of the bob acts vertically downwards, so the work done is negative and its given by
${W_G} = - mgl\left( {1 - \cos \varphi } \right)$.............(3)
Adding (2) and (3) we get the net work done on the bob as
$W = \dfrac{{q\sigma }}{{2{\varepsilon _0}}}l\sin \varphi - mgl\left( {1 - \cos \varphi } \right)$............(4)
Now, according to the work energy theorem, this work done is equal to the change in kinetic energy of the bob from the initial to the final position. So we have
$W = \Delta K$................(5)
Since the bob was at rest initially, so its initial kinetic energy is zero. Also, we know that the velocity of the bob at the extreme position is equal to zero. So the final kinetic energy is also equal to zero. This implies that the total change in the kinetic energy of the bob is equal to zero. Therefore from (5) we have
$W = 0$
From (4)
$\dfrac{{q\sigma }}{{2{\varepsilon _0}}}l\sin \varphi - mgl\left( {1 - \cos \varphi } \right) = 0$
$\Rightarrow \dfrac{{q\sigma }}{{2{\varepsilon _0}}}l\sin \varphi = mgl\left( {1 - \cos \varphi } \right)$
Cancelling $l$ from both the sides, we have
$\dfrac{{q\sigma }}{{2{\varepsilon _0}}}\sin \varphi = mg\left( {1 - \cos \varphi } \right)$
Now, we know that $1 - \cos \varphi = 2{\sin ^2}\dfrac{\varphi }{2}$ and $\sin \varphi = 2\sin \dfrac{\varphi }{2}\cos \dfrac{\varphi }{2}$. Substituting these in the above equation, we get
$\dfrac{{q\sigma }}{{2{\varepsilon _0}}}2\sin \dfrac{\varphi }{2}\cos \dfrac{\varphi }{2} = 2mg{\sin ^2}\dfrac{\varphi }{2}$
$\Rightarrow \dfrac{{q\sigma }}{{{\varepsilon _0}}}\sin \dfrac{\varphi }{2}\cos \dfrac{\varphi }{2} = 2mg{\sin ^2}\dfrac{\varphi }{2}$
Dividing both sides by $\sin \dfrac{\varphi }{2}\cos \dfrac{\varphi }{2}$, we get
$\dfrac{{q\sigma }}{{{\varepsilon _0}}} = 2mg\tan \dfrac{\varphi }{2}$
$\Rightarrow \tan \dfrac{\varphi }{2} = \dfrac{{q\sigma }}{{2mg{\varepsilon _0}}}$
Taking inverse tangent both the sides, we get
$\dfrac{\varphi }{2} = {\tan ^{ - 1}}\left( {\dfrac{{q\sigma }}{{2mg{\varepsilon _0}}}} \right)$
$\Rightarrow \varphi = 2{\tan ^{ - 1}}\left( {\dfrac{{q\sigma }}{{2mg{\varepsilon _0}}}} \right)$............(6)
According to the question, we have
$\Rightarrow \varphi = x{\tan ^{ - 1}}\left( {\dfrac{{\sigma q}}{{2{\varepsilon _0}mg}}} \right)$.......................(7)
Comparing (6) and (7) we finally get
$x = 2$

Hence, the value of $x$ is equal to $2$.

Note: Do not apply the equilibrium to find out the maximum deflection. This is because that will be the deflection, about which the pendulum will oscillate. At the maximum deflection position, the bob will not be in equilibrium but will have a net force towards the equilibrium position.