Question

A simple pendulum makes 10 oscillations in 20 seconds. What is the time period and frequency of its oscillation?

Answer 1

The approach to solve this question is using relation of frequency with time period that is $f = \dfrac{1}{T}$ where f is the frequency and T is the time period, and unitary method , so putting values in formula is easy let us know little about unitary method which will also help you in the further problems.
Let us understand this concept with a basic example, assume that you are going to buy 12 balls cost 20 rupees so, 6 balls cost how many rupees:
For 12 balls we have 20 rupees
$12 \to 20$
For single for we have:
$1 \to \dfrac{{20}}{{12}} = \dfrac{5}{3}$
So, for 6 balls we have,
$6 \to 6 \times$ $\dfrac{5}{3}$ $= 10$ rupees
Based on the above two concepts we will solve our question in an easy way.

Complete solution step by step:

According to the question given let us discuss some of related terms with this question
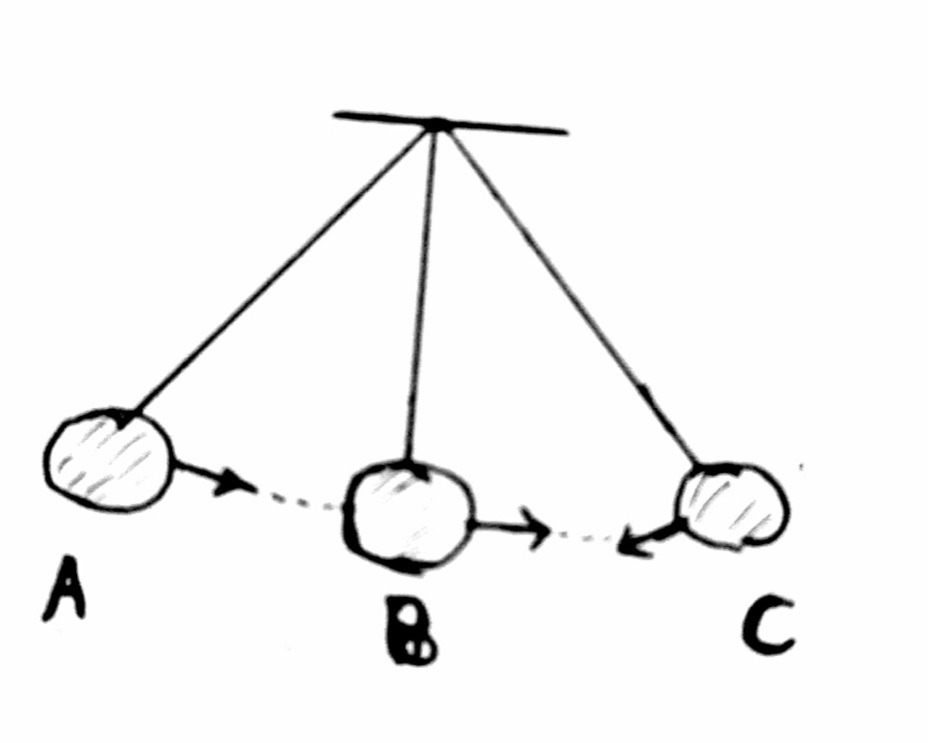
Simple Pendulum is a very small heavy bob suspended at a point from a fixed support using a single thread so that it oscillates freely. The distance between the point of suspension and bob’s centre is
the length of pendulum

One oscillation: One complete to and fro motion of the oscillating body is called one oscillation.
Frequency: It is the number of oscillations made by the body in one second.
Time Period: It is the time taken by a body to complete one oscillation.
So, let's follow the calculations
As mentioned, 10 oscillations in 20 seconds
$10 \to 20 \\\ 1 \to \dfrac{{10}}{{20}} = 0.5\sec \\\$
So, for a single oscillation time taken or what we say time period is 0.5 seconds.
Further calculating frequency
$f = \dfrac{1}{T} \\\ = \dfrac{1}{{0.5}} = 2hz \\\$
So, frequency is 2 hertz.

Note: The motion discussed above is considered in simple harmonic motion.
Let is discuss some important parts regarding this motion:
To study the motion of bob we use sine wave forms which comes from a derivation
The formula used for calculating displacement in simple harmonic motion is
$s = A\sin \omega t$ where A is the amplitude or maximum displacement possible, w is the angular frequency and t is the time take to reach there so, by considering this formula our motion becomes like to and fro like in the diagram given where particle moves from B to C , then C to B , B to A , then back to B and this is called one complete cycle.