Question

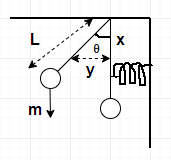
A simple pendulum made up of light rod of length l and bob of mass m has a spring of force constant K connected to it at a distance x below the point of suspension. Find the frequency of vibration of the system

Answer 1

From figure, we can infer that the pendulum has been displaced to an angle $\theta$ during vibration and stretches to a distance y. We can calculate the frequency by finding all the forces that act in this system. Using the angle $\theta$we can resolve forces to its components as well.

Formula used:
Torque $\tau =\overrightarrow{r}\times \overrightarrow{F}=rF\sin \theta$ where $\overrightarrow{r}$the distance is and $\overrightarrow{F}$is the force.

Complete step by step answer:
From the figure, the pendulum has displaced to a length y.
From given, figure we can say that $y=x\tan \theta$. When we consider the small right angled triangle with base x and height y.
For very small angles,
$\begin{aligned} & \tan \theta \sin\theta \\\ & \therefore y=x\theta \\\ \end{aligned}$
Now, restoring force that acts on the spring= $k\theta x$
Torque=$force\times distance$
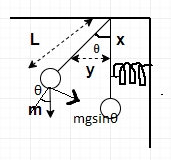
Consider the pendulum bob:
Gravitational force mg acts downwards on the pendulum bob.
Resolving mg, we get the component along the direction of force i.e. $mg\sin \theta$
L is the line of force.
Hence, torque by the bob= $mgL\sin \theta$

Summation of torque by the restoring force :
$\sum{\tau =-(mgL\sin \theta +k\theta x}(x))$(Since the torque by the restoring force acts along a distance x)
For small angles, $\sin \theta \sin \theta$
Hence,

& {{\sum{\tau =-(mgL\theta +k\theta x}}^{2}}) \\\ & =-\theta (mgL+k{{x}^{2}}) \\\ \end{aligned}$$ $\sum{\tau =I\alpha }$ The moment of inertia of pendulum about the point of suspension is $I=m{{L}^{2}}$ The value of angular acceleration $\alpha $is given by $\alpha =-{{\omega }^{2}}\theta $ On substituting the values we get $$\begin{aligned} & I\alpha =-\theta (mgL+k{{x}^{2}}) \\\ & \Rightarrow m{{L}^{2}}\times (-{{\omega }^{2}}\theta )=-\theta (mgL+k{{x}^{2}}) \\\ & \Rightarrow m{{L}^{2}}{{\omega }^{2}}=mgL+k{{x}^{2}} \\\ & \Rightarrow {{\omega }^{2}}=\dfrac{mgL+k{{x}^{2}}}{m{{L}^{2}}} \\\ & \Rightarrow \omega =\sqrt{\dfrac{mgL+k{{x}^{2}}}{m{{L}^{2}}}} \\\ & \\\ \end{aligned}$$ $$\omega $$ can be written as $2\pi f$ Hence, $$\begin{aligned} & 2\pi f=\sqrt{\dfrac{mgL+k{{x}^{2}}}{m{{L}^{2}}}} \\\ & \therefore f=\dfrac{1}{2\pi }\sqrt{\dfrac{mgL+k{{x}^{2}}}{m{{L}^{2}}}} \\\ \end{aligned}$$ This is the value of the frequency of vibration of the system. **Note:** In physics, the restoring force is a force that brings the body in the system back to the position of equilibrium. It is the function of only the position of the mass and directed back towards equilibrium. It is frequently referred in simple harmonic motion