Question

A simple pendulum is oscillating without damping. When the displacement of the bob is less than maximum, its acceleration vector $\vec a$ is correctly shown in:

(A)

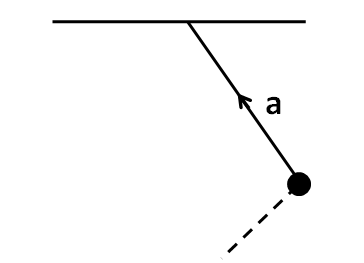
(B)

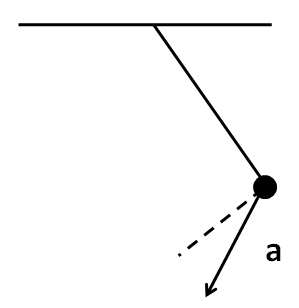
(C)

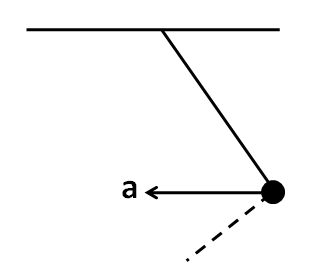
(D)

Answer 1

To solve this question, we need to consider the free body diagram of the bob of the given pendulum at a position when its displacement has a less than maximum value. Then the direction of the acceleration vector will be the same as the direction of the net force.

Formula Used: In this solution we will be using the following formula,
$\Rightarrow {F_{net}} = ma$ where ${F_{net}}$ is the net force acting on a body, $m$ is the mass and $a$ is the acceleration of the body.

Complete step by step answer
Let the length of the string of the pendulum be $L$.
When the displacement of the bob of the pendulum is less than maximum, then the free body diagram of the bob is shown below. Let the velocity of the bob be equal to $v$ at this instant.

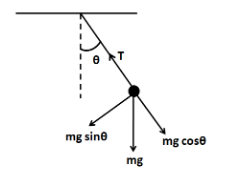
Let the string of the pendulum make an angle of ${{\theta }}$ with the vertical. The forces acting on the bob are
Weight - $mg$
Force of tension - $T$
We have resolved the weight of the bob into radial and tangential directions. Now, we know that the bob of the pendulum undergoes vertical circular motion. So there must be a net centripetal force towards the centre. So from the Newton’s second law we have
$\Rightarrow T - mg\cos {{\theta }} = \dfrac{{m{v^2}}}{L}$
$\Rightarrow {F_R} = \dfrac{{m{v^2}}}{L}$ …………………………...(1)
Here ${F_R}$ is the net force in the radial direction.
Also the net force along the tangential direction is $mg\sin {{\theta }}$. This means that
$\Rightarrow {F_T} = mg\sin {{\theta }}$ ……………………….(2)
So the net force on the bob is given by
$\Rightarrow F = \sqrt {F_R^2 + F_T^2}$
From (1) and (2)
$\Rightarrow F = \sqrt {{{\left( {\dfrac{{m{v^2}}}{L}} \right)}^2} + {{\left( {mg\sin {{\theta }}} \right)}^2}}$ ……………………..(3)
So the net acceleration of the bob is given by
$\Rightarrow a = \dfrac{F}{m}$
From (3)
$\Rightarrow a = \dfrac{1}{m}\sqrt {{{\left( {\dfrac{{m{v^2}}}{L}} \right)}^2} + {{\left( {mg\sin {{\theta }}} \right)}^2}}$
$\Rightarrow a = \sqrt {{{\left( {\dfrac{{{v^2}}}{L}} \right)}^2} + {{\left( {g\sin {{\theta }}} \right)}^2}}$
The direction of this acceleration will be the same as the direction of the net force. The direction of the net force is shown in the figure below.

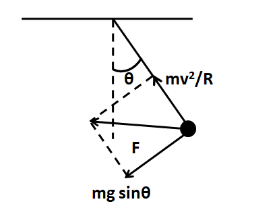
So the direction of the net acceleration is shown as

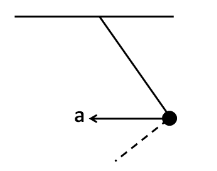
Hence, the correct answer is option C.

Note
In this solution, we have used the parallelogram law to determine the direction of the acceleration of the bob of the pendulum. We can use any one of the laws of vector addition, like the triangular law for this purpose.