Question

A simple pendulum is oscillating with an angular amplitude of ${{60}^{\circ }}$. The ratio of the tension in the string when the bob reaches the mean position and the extreme position respectively is:
A) 2:1
B) 3:1
C) 1:3
D) 4:1

Answer 1

The tension onto the string is a function of the angle made by the string with respect to the mean position. First we need to obtain the expression for tension on the string. Further accordingly we can determine the ratio of the tension in the string when the bob reaches the mean position and the extreme position.

Complete step-by-step solution:

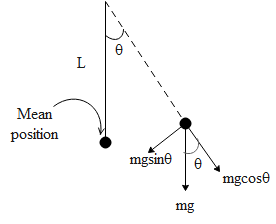
In the above figure we can see a bob of mass ‘m’ suspended to a string of length ‘L’ about the mean position. The angle made by the string with respect to the mean position at any instant be $\theta$. The force due to gravity i.e. mg acts downwards, hence the tension (T) along the string is given by $mg\cos \theta$ and the restoring force is given by $mg\sin \theta$.
The angular amplitude of the above pendulum is given to be as ${{60}^{\circ }}$. Hence the Tension (${{T}_{1}}$ ) in the string at the extreme position is equal to,
$\begin{aligned} & {{T}_{1}}=mg\cos {{60}^{\circ }} \\\ & \because \cos {{60}^{\circ }}=\dfrac{1}{2} \\\ & \therefore {{T}_{1}}=\dfrac{mg}{2} \\\ \end{aligned}$
Similarly the tension ${{T}_{2}}$ in the string at the mean position i.e. $\theta ={{0}^{\circ }}$ is equal to,
$\begin{aligned} & {{T}_{2}}=mg\cos {{0}^{\circ }} \\\ & \because \cos {{0}^{\circ }}=1 \\\ & \therefore {{T}_{2}}=mg \\\ \end{aligned}$
Hence the ratio of the tension in the string at the mean and extreme position is,
$\begin{aligned} & \dfrac{{{T}_{2}}}{{{T}_{1}}}=\dfrac{mg}{\dfrac{mg}{2}} \\\ & \Rightarrow \dfrac{{{T}_{2}}}{{{T}_{1}}}=2 \\\ & \therefore {{T}_{2}}:{{T}_{1}}=2:1 \\\ \end{aligned}$
Therefore the correct answer of the above question is option A.

Note: The tension in the string as the bob moves away from the mean position decreases as the component of gravity acts more in the direction of restoring force. At the mean position, the gravity and the tension become equal. It is also to be noted that for a massless string the tension is constant throughout the string.