Question

A simple pendulum is oscillating with an angular amplitude ${60^ \circ }$ . If mass of bob is $50g$, the tension in the string at mean position is:
Consider: $g = 10m{s^{ - 2}}$, length of the string $L = 1m$ .
A. $0.5N$
B. $1N$
C. $1.5N$
D. $2N$

Answer 1

To solve this question, firstly we have to calculate the velocity of the string by which we can conclude the tension in the string. After getting the value of velocity, we will find the tension in the string with the help of given values.

Complete step by step answer:
Given that:-
The angular amplitude of a pendulum in a string is ${60^ \circ }$.
Mass of bob, $m$ is $50g$ .
And, we have to find the tension in the string, at the mean position.
First, we have to draw the diagram according to the question:

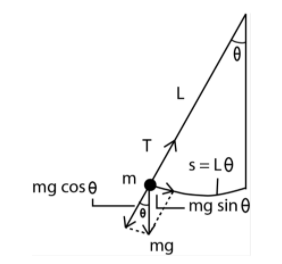
First, find the velocity at the mean position.
So, Loss in Potential Energy = gain in Kinetic Energy
$mgl(1 - \cos {60^ \circ }) = \dfrac{1}{2}m{v^2}$
Now, $m$ and $m$ cancel out from both the sides.
$\Rightarrow \dfrac{{gl}}{2} = \dfrac{{{v^2}}}{2}$
Again, 2 will be canceled from both L.H.S and R.H.S .
$\therefore {v^2} = gl$ or $v = \sqrt {gl}$.
So, the velocity at mean position is $\sqrt {gl}$.
Now, as shown in the diagram, tension in the string at mean position as:
$T = {F_c} + mg$
Here, ${F_c}$ is the centripetal force applied during the tension occurring in the string.
Centripetal Force, ${F_c} = \dfrac{{m{v^2}}}{r}$
$\Rightarrow T = \dfrac{{m{v^2}}}{l} + mg$
$r$ is the length of string as $l$ .
As we found above, use ${v^2} = gl$
$\Rightarrow T = m(\dfrac{{gl}}{l} + g)$
Now, cancel out the $l$
$\Rightarrow T = m(g + g)$
On simplification,
$\Rightarrow T = 2mg$
On substituting the corresponding values, we get
$T = 2 \times 50 \times {10^{ - 3}} \times 10$
$T= 1N$

$\therefore$ The correct option is option (B), the tension in the string at mean position is $1N$.

Note: This might seem obvious but when it is about drawing the forces acting on an object, some often draw the force of tension going towards the wrong direction. Hence, tension can only pull an object. You will be presented with massless ropes and cables in almost every situation in classical mechanics.