Question

A simple pendulum is of length $50cm$. Find time period and frequency of oscillation.$\left( g=9.8m/{{s}^{2}} \right)$.
A. $1.38~sec$ , $0.7246Hz$
B. $2.419sec$,$0.545Hz$
C. $5.619~sec$,$0.6045Hz$
D. $1.419~sec$,$0.7045Hz$

Answer 1

A simple pendulum is a hypothetical apparatus which consists of a point mass m suspended from a weightless, frictionless thread of constant length l and fixed at a pivotal point P. The motion of the body about the string is periodic when displaced to an initial angle of deviation from the original equilibrium position is small, representing a simple harmonic motion.

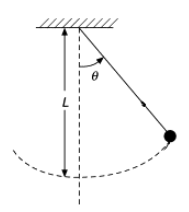
Complete step by step answer:
The information given to us:
Length of the simple pendulum,$l=50cm=0.5m$
And acceleration due to gravity, $g=9.8m/{{s}^{2}}$
The time period of a simple pendulum is given by,
$T=2\pi \sqrt{\dfrac{l}{g}}$
Where l is Length of the simple pendulum
And g is the acceleration due to gravity.
Putting the values in the formula, we get
$T=2\pi \sqrt{\dfrac{0.5}{9.8}}$
$\Rightarrow T=2\pi \sqrt{\dfrac{10}{196}}$
$\Rightarrow T=\dfrac{2\pi }{14}\sqrt{10}$
$\Rightarrow T=\dfrac{\pi }{7}\sqrt{10}$
$\therefore T=1.419$
Therefore, Time period of the simple pendulum, $T=1.419\sec$
As we know, frequency is the inverse of Time Period, thus we can find out frequency of the pendulum by
$\nu =\dfrac{1}{T}$
Putting the values, we get
$\nu =\dfrac{1}{1.419}$
$\therefore \nu =0.745Hz$
Therefore, frequency of the simple pendulum, $\nu =0.745Hz$

Hence, the correct option is option (D)$1.419~sec$, $0.7045Hz$.

Note:
One is advised to convert quantities into their standard units as and when required just like how we have converted few into meters so as to avoid getting an incorrect answer. It is also advised to keep in mind that a simple pendulum is in equilibrium until and unless displaced to an angle, when it swings to and from extreme positions and represents a simple harmonic motion.