Question

A simple pendulum has a time period ${T_1}$ when on the earth’s surface and ${T_2}$ when taken to a height R above the earth’s surface, where R is the radius of the earth. The value of $\dfrac{{{T_2}}}{{{T_1}}}$ is:
A. 1
B. $\sqrt 2$
C. 4
D. 2

Answer 1

A simple pendulum is an instrument consisting of a mass suspended to it through a weightless tread whose length is constant. The time period is the time required by a body exhibiting periodic motion to complete one cycle of motion. In a simple pendulum, it is total time to make a left and a right swing. Here period depends upon the length of the pendulum. Given as
$T = 2\pi \sqrt {\dfrac{l}{g}}$
In this question, find the time period of the pendulum is on the earth’s surface and also when the pendulum is at height R from the earth’s surface, and they find their ratio.

Complete step by step answer:
It is given that the radius of the earth is R, and then the pendulum is moved R above the earth surface
We know the time period of a simple pendulum is given as
$T = 2\pi \sqrt {\dfrac{l}{g}}$
From the given formula, we can conclude that
$T \propto \dfrac{1}{{\sqrt g }}$
Hence we can say the ratio
$\dfrac{{{T_2}}}{{{T_1}}} = \dfrac{{\sqrt {{g_1}} }}{{\sqrt {{g_2}} }} - - - (i)$

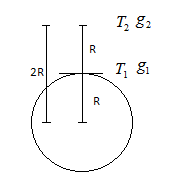
The gravitational force on the pendulum at the earth's surface will be ${g_1} = \dfrac{{GM}}{{{R^2}}}$,
where G is the gravitational constant
Now the gravitational force on the pendulum when it is at a height R above the earth surface

$${g_2} = \dfrac{{GM}}{{{{\left( {2R} \right)}^2}}} \\\ = \dfrac{{GM}}{{4{R^2}}} \\\$$

Now put ${g_1}$and ${g_2}$, we get

$$\dfrac{{{T_2}}}{{{T_1}}} = \dfrac{{\sqrt {{g_1}} }}{{\sqrt {{g_2}} }} \\\ = \sqrt {\dfrac{{GM}}{{{R^2}}} \times \dfrac{{4{R^2}}}{{GM}}} \\\ = \sqrt 4 \\\ = 2 \\\$$

Hence, the value of $\dfrac{{{T_2}}}{{{T_1}}}$=2.

So, the correct answer is “Option D”.

Note:
Students must not get confused while finding a time period of the pendulum of different masses at different heights since the time period does not depend on the mass. When this pendulum is displaced sideways from its equilibrium position, it is subjected to a restoring force gravity, which will accelerate it back towards the equilibrium position.