Question

A simple pendulum consists of a light string from which a spherical bob of mass $M$ is suspended. The distance between the point of suspension and center of the bob is $l$ the bob is initial velocity $v$ in equilibrium position (at the lowest point). What can be the maximum velocity $v$, so that the pendulum oscillates without the string becoming slack?
A. $\sqrt {gl}$
B. $\sqrt {2gl}$
C. $\sqrt {4gl}$
D. $\sqrt {5gl}$

Answer 1

In order to solve this question we need to understand energy conservation. Energy can never be created nor can it be destroyed rather it can only be transferred from one form to another. Energy conservation states that only when the work done by mechanical force is zero then increase in kinetic energy is equal to decrease in potential energy or decrease in kinetic energy is equal to increase its potential energy.

Complete step by step answer:
According to the question, the mass of the pendulum bob is given as, $M$. And the initial velocity of bob is, $u = v$. So to find the maximum velocity of bob such that string does not become slack, we know the maximum angular displacement is $\alpha = \dfrac{\pi }{2}$ here, $\alpha$ is angular displacement of bob from mean position.

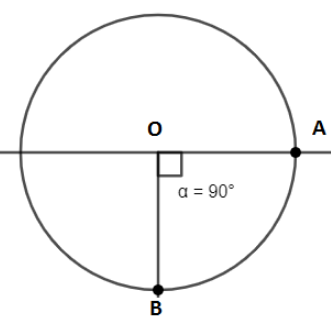
So the string becomes horizontal at max position that is at point A. Since the work done by mechanical force is zero as there is no friction and gravitational force is conservative force, so we apply energy conservation. Let the final velocity at horizontal position A be, “V”.Since at final position, bob stops so, $V = 0\,m{\sec ^{ - 1}}$.

Also let the bob raises by height, “h” up to maximum position
So, this maximum height is equal to string length
Since, perpendicular distance $AB = h$ and $OB = l$ so, $h = l$
So increase in potential energy is given as, $\Delta U = {U_A} - {U_B}$
${U_A} = Mgh$ Or, ${U_A} = Mgl$
$\Rightarrow {U_B} = 0$ (Assuming that mean position is reference point to measure potential)
So putting values we get, $\Delta U = Mgl$.

And decrease in Kinetic energy is given by, $\Delta K.E = K.{E_B} - K.{E_A}$.
Since, $K.{E_B} = \dfrac{1}{2}M{u^2}$ and $K.{E_A} = \dfrac{1}{2}m{v^2}$
So, $\Delta K.E = \dfrac{1}{2}M{u^2} - \dfrac{1}{2}M{V^2}$
Putting values we get,
$\Delta K.E = \dfrac{1}{2}M{v^2} - 0$
$\Rightarrow \Delta K.E = \dfrac{1}{2}M{v^2}$
So according to law of energy conservation we get,
$\Delta K.E = \Delta U$
Putting values we get,
$\dfrac{1}{2}M{v^2} = Mgl$
$\Rightarrow {v^2} = 2gl$
So the speed is, $v = \sqrt {2gl}$

So the correct option is B.

Note: It should be remembered that here the work done by mechanical force is zero because here is no dissipative force which acts on the bob and thereby restricting its motion, also gravitational force is a conservative force means the potential is time independent and it is only depends on the space . Similarly if no net force acts on the body then its momentum is conserved.