Question

A signal of $20mV$ is applied to a common emitter amplifier circuit. Due to this, the change in base current and the change in collector current are $20\mu A$ and $2mA$. The load resistance is $10k\Omega$ , transconductance is:
A) $0.1{\Omega ^{ - 1}}$
B) $0.2{\Omega ^{ - 1}}$
C) $10{\Omega ^{ - 1}}$
D) None of these

Answer 1

In this question, we have the change in collector current $\Delta I{}_C$ and a signal which is added to the base-emitter voltage $\Delta {V_{BE}}$. We can use ${g_m} = \dfrac{{\Delta I{}_C}}{{\Delta {V_{BE}}}}$to find the transconductance ${g_m}$ of the common emitter amplifier circuit.

Complete step by step solution:
According to the question, a signal of $20mV$ is applied to a common emitter amplifier circuit which means $20mV$ is added to the base-emitter voltage($\Delta {V_{BE}}$). The load resistance ${R_L}$ in the common emitter amplifier circuit is $10k\Omega$. The change in base current $\Delta {I_B}$ is $20\mu A$ and the change in collector current $\Delta I{}_C$ is $2mA$.
We know that if $\Delta {V_{BE}}$ is bas-emitter voltage and $\Delta I{}_C$ is the collector current, then the transconductance ${g_m}$ of the common emitter amplifier circuit is given as-
${g_m} = \dfrac{{\Delta I{}_C}}{{\Delta {V_{BE}}}}$
Now, putting the values of $\Delta I{}_C = 2mA$ and $\Delta {V_{BE}} = 20mV$ in the equation, we get-
${g_m} = \dfrac{{2mA}}{{20mV}} \\\ \Rightarrow {g_m} = \dfrac{1}{{10}}{\Omega ^{ - 1}} \\\ \Rightarrow {g_m} = 0.1{\Omega ^{ - 1}} \\\$
Therefore, the transconductance of the common emitter amplifier circuit is $0.1{\Omega ^{ - 1}}$.

Hence, option A is correct.

Additional Information:

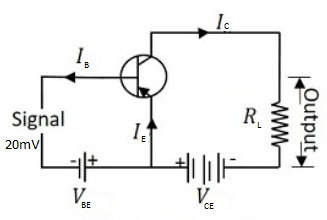
Above diagram shows a common emitter transistor. In this transistor, an emitter is common in both input circuit and output circuit. The base and emitter make the input circuit. The collector and the emitter make the output circuit. The input voltage is known as base-emitter voltage $\Delta {V_{BE}}$ and the output voltage is known as emitter-collector voltage $\Delta {V_{CE}}$. We can get the output current at the load resistance ${R_L}$.

Note: In this question, two types of change in current are given. We can calculate transconductance by using $\Delta I{}_C$ and $\Delta {V_{BE}}$. $\Delta {I_B}$ is not used in the calculation of transconductance. $\Delta {I_B}$ is used with $\Delta I{}_C$ to calculate the current gain of the circuit. The unit of the transconductance is always ${\Omega ^{ - 1}}$.