Question

A signal generator supplies a sine wave of $20\,\,V$, $5\,\,KHz$ to the circuit shown in the figure. Then choose the right statement.

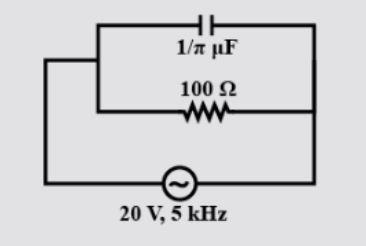
A) the current in the resistive branch is $0.2\,\,A$.
B) the current in the capacitive branch is $0.126\,\,A$.
C) total line current is $0.283\,\,A$.
D) current in both the branches are the same.

Answer 1

The given problem can be solved using the formula derived for the capacitive resistance of the capacitor and the current in each branch is found using the formula derived from the law of Ohm’s law which incorporates the resistance of the resistor, current across the circuit and the potential difference a ross the circuit.

Useful solution:
The formula for the capacitive resistance of the capacitor is;
${X_C} = \dfrac{1}{{\omega C}}$
Where, ${X_C}$ denotes the capacitive resistance, $\omega$ denotes the angular voltage, $C$capacitance of a capacitor.

Complete step by step solution:
The data given in the problem are;
A signal generator supplies a sine wave of voltage, $V = 20\,\,V$;
Frequency of the generator is, $f = 5\,\,KHz$.
Capacitance of the capacitor is, $C = \dfrac{1}{\pi }\,\,\mu F$.
Resistance of the resistor is, $R = 100\,\,\Omega$.

The formula for the capacitive resistance of the capacitor is;
${X_C} = \dfrac{1}{{\omega C}}$
Where, ${X_C}$ denotes the capacitive resistance, $\omega$ denotes the angular voltage, $C$capacitance of a capacitor.
Where $\omega = 2\pi f$
${X_C} = \dfrac{1}{{2\pi fC}}$
Substitute the values of frequency of the generator, angular voltage and the capacitance of the capacitor.
${X_C} = \dfrac{1}{{\dfrac{{2 \times \pi \times 5000}}{\pi }}} \\\ {X_C} = {10^{ - 4}}\,\,\Omega \\\$
Here, the resistance is very high in comparison to capacitive reactance, so almost the whole current will pass through the resistor.
Current through resistor of $100\,\,\Omega$ is,
$I = \dfrac{V}{R} \\\ \\\$
Where, $I$ denotes the current in the circuit, $V$ denotes the potential difference across the circuit, $R$ denotes the resistance across the resistor.
Substitute the value of the voltage and the resistor;
$I = \dfrac{{20\,\,V}}{{100\,\,\Omega }} \\\ I = \dfrac{{20}}{{100}} \\\ I = 0.2\,\,A \\\$

Therefore, the current across the resistive branch is found as $I = 0.2\,\,A$

Hence, the option (A) the current in the resistive branch is $I = 0.2\,\,A$.

Note: Signal generator is an electronic device that gives quality test signals like sine wave, square wave, triangular wave and etc. The signal generator that gives out the periodic signal that has a frequency of Audio Frequency (AF) range is called AF signal generator.