Question
Question: A shot is fixed from O at an angle \(\alpha \) with horizontal. If the shot hits the object P on an ...
A shot is fixed from O at an angle α with horizontal. If the shot hits the object P on an inclined plane horizontally then the relation between αand β is
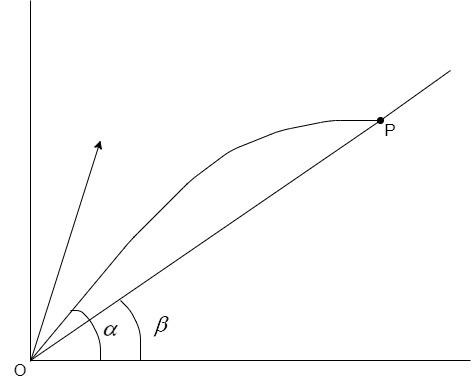
A. tanα=2tanβ
B. tanα=2tanβ
C. tanα=4tanβ
D. tanα=4tanβ
Solution
To solve this question, it is important to understand the concept of maximum height and range of a projectile and the relationship between them.
The maximum height is the topmost point achieved by the projectile at exactly, half of the range, which is the total horizontal distance covered by the object.
The relation among the two is, at the maximum height of the projectile, the horizontal distance covered will be equal to half of the total range.
Complete step by step answer:
The projectile motion is a 2-dimensional motion of a body that is projected or thrown off, from the Earth’s surface with sufficient initial velocity and at an acute angle. Examples of projectile motion are kicking a stationary football during a penalty shootout and launching of ground to air missiles.
There are three main parameters to be studied in the motion of a projectile. They are:
i) Time of flight: It is the time taken for the projectile from its launch to hit the ground.
ii) Height of projectile: It is the maximum vertical distance reached by the projectile.
iii) Range: It is the maximum horizontal distance covered by the projectile.
If u is the initial velocity of the projectile and θ is the angle of the projectile,
Maximum height of projectile, H=2gu2sin2θ
Range of projectile, R=gu2sin2θ
Consider a shot fired at point O with an angle of α.
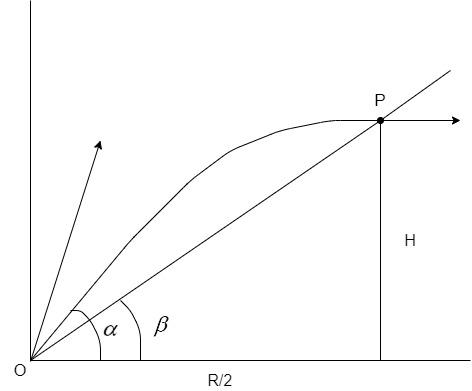
Here, it is given in the figure that the shot hits the point P horizontally. Usually, the projectile will have two components of velocity – horizontal and vertical. At the topmost point of the projectile i.e. maximum height of the projectile, there is no vertical component of the velocity and only horizontal component exists. Given that the velocity at P is horizontal, it proves that the point P is maximum height (H).
The maximum height occurs at exactly, half of the horizontal range (R) as shown in the figure.
From the figure,
tanβ=2RH
⇒tanβ=R2H
With α being the angle of attack of the projectile, substituting for height H in the above equation,
tanβ=R2H
⇒tanβ=2g×R2u2sin2α
Substituting for R,
tanβ=2g×R2u2sin2α
⇒tanβ=2g×u2sin2α2u2sin2α×g
⇒tanβ=sin2αsin2α
sin2α=2sinαcosα
Substituting, we get –
tanβ=2sinαcosαsin2α
⇒tanβ=2cosαsinα
⇒tanβ=2tanα
∴tanα=2tanβ
Hence, the correct option is Option B.
Note:
In the formula for range R, if we substitute θ=45∘, we get –
R=gu2sin2θ=gu2sin(2×45∘)=gu2sin90=gu2
This is the maximum value of range.
Thus, the range is maximum if the angle of attack is at θ=45∘ for a particular velocity. This is why you can see that in football, during the long shoots, the person shooting the ball makes sure the angle of kicking is nearly equal to 45∘ so that the ball travels to a very distant place in the football field.
