Question

A shot is fired with a velocity $200\,{\text{m}}{{\text{s}}^{ - 1}}$ in a direction making an angle of $60^\circ$ with the vertical. What will be its time of flight and horizontal range? (take $g = 10\,{\text{m}}{{\text{s}}^{ - 2}}$ )

Answer 1

First of all, we will draw the diagram as given in the question. Then we will take the angle which is being formed with the horizontal, into account. Now we can apply the respective formulae to calculate the results.

Complete step by step answer:
In the given problem, we are supplied with the following data:
The velocity of the shot at which it was fired was $200\,{\text{m}}{{\text{s}}^{ - 1}}$ .
The angle which the shot makes with the vertical is $60^\circ$ .
We are asked to find out the time of flight and the horizontal range of the shot.
Here, the time of flight means the time from which the object is projected to the time it hits the earth. Again, the horizontal range is the distance of the surface of the earth at which the projected object hits the ground. To begin with, according to the scenario we draw a diagram for better understanding.

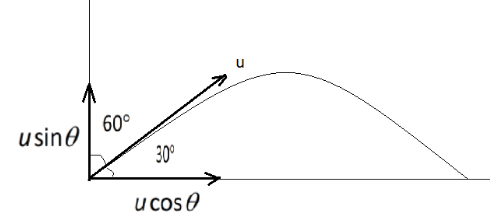
From the diagram, it is clear that the direction of velocity of the shot is at an angle $60^\circ$ with the vertical and hence, the angle with the horizontal is $30^\circ$ . The vertical component of velocity is $200\sin \theta$ while the horizontal component is $200\cos \theta$ .
Now, we apply the formula which gives the time of flight of a projectile:
$T = \dfrac{{2u\sin \theta }}{g}$ …… (1)
Where,
$T$ indicates the time of flight.
$u$ indicates the initial velocity.
$\theta$ indicates the angle between the direction of velocity of the projectile and the horizontal.
$g$ indicates the acceleration due to gravity.
So, we substitute the required values in the equation (1), we get:
T = \dfrac{{2u\sin \theta }}{g} \\\ \Rightarrow T = \dfrac{{2 \times 200 \times \sin 30^\circ }}{{10}} \\\ \Rightarrow T = 2 \times 20 \times \dfrac{1}{2} \\\ \Rightarrow T = 20\,{\text{s}} \\\
Hence, the time of flight of the shot is found out to be $20\,{\text{s}}$ .
To calculate the horizontal range, we use the formula as given below:
$R = \dfrac{{{u^2}\sin 2\theta }}{g}$ …… (2)
Where,
$R$ indicates the horizontal range.
$u$ indicates the initial velocity.
$\theta$ indicates the angle between the direction of velocity of the projectile and the horizontal.
$g$ indicates the acceleration due to gravity.
So, we substitute the required values in the equation (2), we get:
$R = \dfrac{{{u^2}\sin 2\theta }}{g} \\\ \Rightarrow R = \dfrac{{{{\left( {200} \right)}^2}\sin \left( {2 \times 30^\circ } \right)}}{{10}} \\\ \Rightarrow R = \dfrac{{200 \times 200 \times \sin 60^\circ }}{{10}} \\\ \Rightarrow R = 200 \times 20 \times \dfrac{{\sqrt 3 }}{2} \\\ \Rightarrow R = 100 \times 20 \times \sqrt 3 \\\ \therefore R = 2000\sqrt 3 \,{\text{m}} \\\$
Hence, the horizontal range is found out to be $2000\sqrt 3 \,{\text{m}}$.

Note: This problem is based on the projectile motion. While solving this problem, many students tend to make mistakes by taking the angle as $60^\circ$ in the formula, which is wrong. Rather we must take the angle with the horizontal. Using the angle $60^\circ$ will definitely produce irrelevant results.