Question

A shot is fired at an angle $\theta$ to the horizontal such that it strikes the hill while moving horizontally. Find the initial angle of projection $\theta$ :
A. $\theta = {\tan ^{ - 1}}\left( {\dfrac{2}{5}} \right)$
B. $\theta = {\tan ^{ - 1}}\left( {\dfrac{3}{8}} \right)$
C. $\theta = {\tan ^{ - 1}}\left( {\dfrac{3}{2}} \right)$
D. $\theta = {53^ \circ }$

Answer 1

Here we have to first find the horizontal and vertical components and then use both the 1st and the 2nd equations of motion to get the final answer.
1st equation of motion: To find the final velocity, initial velocity, acceleration and time we will use the 1st equation of motion.
2nd equation of motion: the displacement of an object under constant acceleration is given by the second equation of motion

Complete step by step answer:

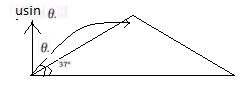
According to the question the velocity at the top of the hill will be parallel to the velocity at the ground.
We know that while moving horizontally at maximum height, there will only be horizontal velocity and the vertical velocity will be zero.
Now if the shot is fired from $u\sin \theta$, then also the vertical velocity will be zero for time $t$.
So, the final velocity in this case will be zero and the acceleration due to gravity $g$ will act against $u\sin \theta$.
We know that,
According to first equation of motion:
$v = u + at \\\ 0 = u\sin \theta - gt \\\$

$t = \dfrac{{u\sin \theta }} {g}$ ...... (i)
The horizontal and vertical components against $u\sin \theta$ and $g$ would be $u\sin \left( {\theta - 37} \right)$ and $- g\cos 37$.
The distance here is considered as zero since the vertical displacement is zero.
According to third equation of motion:
$s = ut + \dfrac{1}{2}a{t^2}$
Putting the values we get:
$0 = u\sin \left( {\theta - 37} \right)t + \dfrac{1} {2}\left( { - g\cos 37} \right){t^2}$
$\Rightarrow t = \dfrac{{2u\sin \left( {\theta - 37} \right)}} {{g\cos 37}}$ ......(ii)
Hence, from equations (i) and (ii) we get-
\dfrac{{u\sin \theta }} {g} = \dfrac{{2u\sin \left( {\theta - 37} \right)}} {{g\cos 37}} \\\ \sin \theta = \dfrac{{2\sin \left( {\theta - 37} \right)}} {{\dfrac{4} {5}}} \\\
\implies 4\sin \theta = 10\sin \left( {\theta - 37} \right) \\\
\implies 4\sin \theta = 8\sin \theta - 6\cos \theta \\\
\implies 4\tan \theta = 6 \\\
\implies \tan \theta = \dfrac{3} {2} \\\
$\therefore \theta = {\tan ^{ - 1}}\left( {\dfrac{3} {2}} \right) \\\$

So, the correct answer is “Option C”.

Note:
Here we have to be careful while writing the equations as the equations are complicated and we may tend to make some mistakes.
Similarly for this question as the shot is moving horizontally, so the vertical velocity would be zero at the top of the hill.