Question
Question: A shot is fired at \({30^0}\) with the vertical from a point on the ground with kinetic energy K. If...
A shot is fired at 300 with the vertical from a point on the ground with kinetic energy K. If air resistance is ignored, the kinetic energy at the top of the trajectory is:
A) 43K
B) 2K
C) K
D) 4K
Solution
We are going to find out the kinetic energy at top. Then we will make the vector component of the bullet. The sine function will get canceled as gravity is working against it. The bullet will move along cos function, and with the help of kinetic energy is K=21mv2 and K’ at 60o we will find out the answer.
Complete step by step answer:
Step 1:
Before solving the question let us understand some basic things.
Projectile motion is a form of motion experienced by an object or particle (a projectile) that is projected near the Earth's surface and moves along a curved path under the action of gravity only (in particular, the effects of air resistance are assumed to be negligible).
When a particle is projected obliquely near the earth’s surface, it moves simultaneously in the direction of horizontal and vertical. The motion of such a particle is called Projectile Motion. In the below diagram, where a particle is projected at an angleθ =45o with an initial velocity u.
Step 2:
Now coming to the question:
To understand it we will consider a diagram depicting the language of question for better understanding.
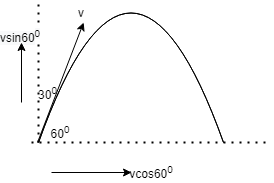
Here in the diagram a shot is fired at 300 with the vertical from a point on the ground with kinetic energy K.
The path will be parabolic and we have separated into the sine and cosine components as seen in the diagram.
The sine component will come to zero as gravity is acting on it and hence only vcos600 will remain for the motion.
Initial kinetic energy is K=21mv2 ….. (1)
Now we will calculate the kinetic energy at the top most point. It will be k’=21m(vcos600)2
The value of cos600=21 putting it in above equation we will get k’=81mv2 …….. (2)
Dividing equation 1 and 2 we get kk′=21mv281mv2
Which on simplification will give, K’=4k
Hence, the kinetic energy at the top of the trajectory is 4k
So option, D is correct.
Note: In projectile motion the maximum horizontal range can be obtained when an object is thrown at an angle of 45o and here the range will be maximum for the stone. For maximum horizontal range Rm=gv2, g is the gravity constant and v is velocity.
