Question

A short bar magnet is placed in a horizontal plane with its axis in the magnitude meridian. Null points are found on its equatorial line at $12.5\,cm$ from the center of the magnet. The earth’s magnetic field at the place is $0.38G$ and the angle of dip is zero.
$(i)$What is the total magnetic field at points on the axis of the magnet located at the same distance $(12.5)$ from the center?
$(ii)$ Locate the null points when the magnet is turned around by ${180^ \circ }$

Answer 1

The pole strength and distance between the two poles are dependent on the product. Here The distance between a magnetics two poles then we know the equatorial line point value, the magnet center and also the magnetic field angle, so we can solve the above two statements.

Useful formula:
Magnetic field on the normal bisector at a distance,
$r$ from the center is given by $\overrightarrow {{B_e}} = - \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{\overrightarrow M }}{{{r^3}}}$
Where,
${B_e}$ at axial point,
$\overrightarrow M$ is a magnetic dipole,
${\mu _0}$ is a null point

Complete step by step solution:
Given by,
Equatorial line at $12.5\,cm$
Magnetic field at the place is $0.38\,G$

Figure A
It is known that when the magnet's north and south poles face magnetic north and south respectively, null points are obtained on the usual bisector.
At a distance, the magnetic field on the standard bisector $r$ from the center is given by $\overrightarrow {{B_e}} = - \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{\overrightarrow M }}{{{r^3}}}$
Provided $r$ is much greater than the length of the magnet.
At a null point,
This field is balanced by the earth’s field.
So,
${B_e} = {B_H}$,
$\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{\overrightarrow M }}{{{r^3}}} = 0.38 \times {10^4}$…………… $(1)$
Since the dip angle $(S)$ is zero,
Here,
Therefore,
${B_v} = 0$
The horizontal part of the field of the earth equals the field itself.
Next,
Magnetic field due to a magnet at a distant point on its axis $r$ from the center is given by
${B_a} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{r^3}}}$………………………….$(2)$
This is much larger than the length of the magnet $r$ given.
Then,
The above equation only applies strictly to a point dipole from fig A
It is apparent that on the axis, this field adds up to the field of the planet,

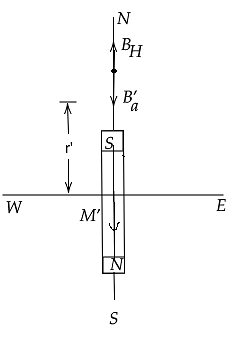
Figure B
Thus, the total field at a point on the axis has a magnitude equal to ${B_a} + {B_H}$
$\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{r^3}}} + 0.38 \times {10^4}$…………..$(3)$
According to the $\overrightarrow M$
Which is parallel to the field of the earth in case A
Thus, the same distance on the axis as the null point distance, the total area, using the same distance on the axis as the null point distance.
Equation $(1)$ and $(3)$
We get,
$2 \times 0.38 \times {10^{ - 4}} + 0.38 \times {10^{ - 4}}$
On simplifying,
$3 \times 0.38 \times {10^{ - 4}}$
Again solving,
$1.14 \times {10^{ - 4}}\,tesla$
This field is directed along $\overrightarrow M$.
Hence,
We did not require that given value of $12.5\,cm$ for the null point distance, except in so far that this was assumed to be much greater than the length of the magnet.
$(ii)$
When the bar I turned around by ${180^ \circ }$,the magnetic north and south poles face magnetic south and north respectively.
In this case,
$\overrightarrow M$ is antiparallel to the earth’s field. From fig B
It is clear that the null point now lies on the axis of the magnet at a distance $r'$ given by,
${B_a}' = {B_H}$ or $\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{r{'^3}}} = 0.38 \times {10^4}$……………$(4)$
Comparing equation $(4)$ and $(1)$,
We get,
$\dfrac{2}{{r{'^3}}} = \dfrac{1}{{{r^3}}}\,$ or $r{'^3} = 2{r^3}$
Here,
The value of $r = 12.5\,cm$ , $r' = 15.7\,cm$

Note: In the anticlockwise direction, the electrons revolve while the current spins in the clockwise direction. This electron motion produces a south pole and a north pole, resulting in the action of the atom as a magnetic dipole. Most elementary particles operate as magnetic dipoles inherently.