Question

A short bar magnet has a magnetic moment of $0.48J{{T}^{-1}}$. Give the direction and magnitude of the magnetic field produced by the magnet at a distance of 10 cm from the centre of the magnet on (a) the axis, (b) the equatorial lines (normal bisector) of the magnet.

Answer 1

Hint: We can find the formulas of the magnetic field at each direction from the Biot-Savart's law. Magnetic moments can be written as the product of current and area. After finding the formulas we can assign the given values to the solution. In each case, the direction of the magnetic field will be different.

Formula used:
$\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m\times 1}{{{d}^{2}}}$, where m is the pole strength, d is the distance between the north pole and the point and ${{\mu }_{0}}$ is the permeability of free space.

Complete step by step answer:
Let us consider a bar magnet of length 2l and centre O. Let a point P lie on the axial line at a distance from the centre of the magnet.

Here south and the north pole of the magnet applying a magnetic field on the point will be different. We can add these two fields to find the net magnetic field acting on the point. We can say that m is the pole strength. Magnetic field strength due to north pole at the point P can be written as,
${B}'=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m\times 1}{{{(d-l)}^{2}}}$, where m is the pole strength, (d-l) is the distance between the north pole and the point and ${{\mu }_{0}}$ is the permeability of free space.
${B}'=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m}{{{(d-l)}^{2}}}$………………………………(1)
The magnetic field strength due to the south pole at the point P can be written as,
${B}''=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m}{{{(d+l)}^{2}}}$, where m is the pole strength, (d+l) is the distance between the south pole and the point, and ${{\mu }_{0}}$ is the permeability of free space.
Therefore, the net magnetic field acting on the point is,
$B={B}'-{B}''$
We can assign the calculated values into this.
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m}{{{(d-l)}^{2}}}-\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m}{{{(d+l)}^{2}}}$
$B=\dfrac{{{\mu }_{0}}m}{4\pi }\left[ \dfrac{1}{{{(d-l)}^{2}}}-\dfrac{1}{{{(d+l)}^{2}}} \right]$
$B=\dfrac{{{\mu }_{0}}m}{4\pi }\left[ \dfrac{{{(d+l)}^{2}}-{{(d-l)}^{2}}}{{{({{d}^{2}}-{{l}^{2}})}^{2}}} \right]$
$B=\dfrac{{{\mu }_{0}}m}{4\pi }\left[ \dfrac{4ld}{{{({{d}^{2}}-{{l}^{2}})}^{2}}} \right]$
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2Md}{{{({{d}^{2}}-{{l}^{2}})}^{2}}}$, since $m\times 2l=M$, where $M$ is the magnetic dipole moment.
Since we are dealing with a tiny bar magnet, we can neglect the length of the magnet from the equation.
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2Md}{{{d}^{4}}}$
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2M}{{{d}^{3}}}$………………..(2)
Next, we can find out the magnetic field strength at a point on the equatorial line of the bar magnet.

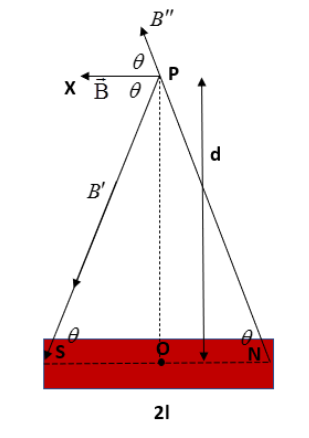
Here the point P lies at a distance ‘d’ from the centre of the bar magnet. The magnetic field strength on the point P due to the south pole can be written as,
${B}'=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m}{({{d}^{2}}+{{l}^{2}})}$………………………..(3)
The magnetic field strength at point P due to the north pole of the bar magnet can be written as,
${B}''=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{m}{({{d}^{2}}+{{l}^{2}})}$……………………….(4)
Here, the net magnetic field acts in an angle $\theta$ to each magnetic field. Therefore, the net magnetic field can be written as,
$B={B}'\cos \theta +{B}''\cos \theta$
Here we can see, the magnetic field due to the north and south pole are the same.
$B=2{B}'\cos \theta$
$\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$
$\cos \theta =\dfrac{l}{\sqrt{\left( {{d}^{2}}+{{l}^{2}} \right)}}$
Therefore the magnetic field will be,
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{2m}{{{(d+l)}^{2}}}\dfrac{l}{\sqrt{\left( {{d}^{2}}+{{l}^{2}} \right)}}$
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{M}{{{({{d}^{2}}+{{l}^{2}})}^{\dfrac{3}{2}}}}$
Since we are dealing with a tiny bar magnet, we can remove the length of the bar magnet.
$B=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{M}{{{d}^{3}}}$……………………….(5)
As per the given details,
Magnetic moment of bar magnet, $M = 0\text{.48J}{{\text{T}}^{-1}}$
Distance from the point to centre of the magnet, $d = 10cm$
To find the magnetic field along the axis, we can assign these values to the equation (2)
${{B}_{a}}=\dfrac{4\pi \times {{10}^{-7}}}{4\pi }\dfrac{(2\times 0.48)}{{{0.1}^{3}}}$
${{B}_{a}}=0.96\times {{10}^{-4}}T$
This magnetic field is along the south-north direction
To find the magnetic field along the equatorial line, we can assign the above values to the equation (5)
${{B}_{e}}=\dfrac{4\pi \times {{10}^{-7}}}{4\pi }\dfrac{0.48}{{{0.1}^{3}}}$
${{B}_{e}}=0.48\times {{10}^{-4}}T$
This magnetic field is along the north-south direction.

Note: In the axial direction, we are finding the net magnetic field as the difference between the magnetic field due to the north pole and magnetic field south pole. Since they are applying fields in opposite directions. In the axial direction, the magnetic field will be in the same direction of its magnetic dipole moment vector. But in equatorial lines, The magnetic field is opposite to the magnetic dipole moment vector. It is advised to learn the formulas directly. So the derivation part is not required. It is easy to remember the magnetic field on the equatorial line if the axial magnetic field is known. Since the magnetic field will be half of the magnetic field along the axial line.