Question

A ship is travelling due east at a speed of 10 km/hr. Calculate the speed of the boat heading ${30^0}$ east of north if it appears always moving due north from the ship.
(A) $10\sqrt 2$ km/h
(B) 10 km/h
(C) 20 km/h
(D) 3 km/h

Answer 1

This could be simply solved by taking the components of speed in north and east direction. From there we need to find the option which matches our answer.

Formula used: Here, we will use the basic formula of taking components:
${{{v}}_{{x}}}{{ = vcos}}\theta$
${{{v}}_{{y}}}{{ = vsin}}\theta$ .

Complete step by step answer:
We will start by assuming ship ${{{S}}_{{1}}}$ in east direction and ${{{S}}_{{2}}}$ along north direction.

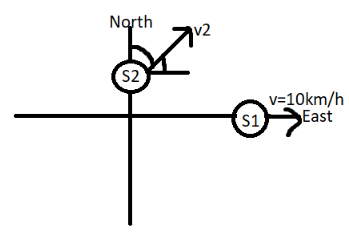
We already know that,
${{{v}}_{{1}}}{{ = 10km/h}}$
Similarly, ${{{v}}_{{2}}}$ makes ${60^0}$ with the east axis.
On resolving the components along east axis:
${{{v}}_{{2}}}{{cos6}}{{{0}}^{{0}}}{{ = }}{{{v}}_{{1}}}$
${{{v}}_{{2}}}{{ = 2}}{{{v}}_{{1}}}{{ = 2}} \times {{10 = 20km/h}}$
So, we need to select the correct option.
Thus, the correct option is C.

Additional Information
Speed is a scalar quantity that refers to "how fast an object is moving." Speed can be thought of as the rate at which an object covers distance. The first scientist to measure speed as distance over time was Galileo.

Note:
It should be always kept in mind that while taking the components that cosine and sine functions are taken properly. Vector quantities are often represented by scaled vector diagrams. Vector diagrams depict a vector by use of an arrow drawn to scale in a specific direction. Vector diagrams were introduced and used in earlier units to depict the forces acting upon an object. Such diagrams are commonly called free-body diagrams.
Vectors can be directed due East, due West, due South, and due North. But some vectors are directed northeast and some vectors are even directed northeast, yet more north than east. Thus, there is a clear need for some form of a convention for identifying the direction of a vector that is not due East, due West, due South, or due North.