Question

A ship A is moving Westwards with a speed of $10km/h$ and a ship B $100km$ South of A is moving northwards with a speed of $10km/h$. The time after which the distance between them becomes shortest is:

& A)0h \\\ & B)5h \\\ & C)5\sqrt{2}h \\\ & D)10\sqrt{2}h \\\ \end{aligned}$$

Answer 1

Here, the velocities of ships A and B are given. From this, we can find the velocity of A with respect to B. Then, draw a vector diagram and mark the distances and angles. Consider the triangle made by the resultant velocity and the path of ship B and find out all the sides and thereby the time taken by the ships to reach their shortest distance can be calculated.
Formula used:
$\text{time = }\dfrac{\text{distance}}{\text{velocity}}$

Complete step by step answer:

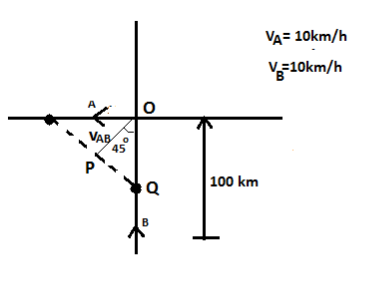
Velocity of A with respect to B is,
${{\vec{v}}_{AB}}={{\vec{v}}_{A}}-\left( -{{{\vec{v}}}_{B}} \right)={{\vec{v}}_{A}}+{{\vec{v}}_{B}}$
Then,
${{v}_{AB}}=\sqrt{{{v}_{A}}+{{v}_{B}}}$ ------- 1
Given that,
Velocity of A, ${{v}_{A}}=10km/h$
Velocity of B, ${{v}_{B}}=10km/h$
Substitute the velocities of ships A and B in equation 1 we get,
Velocity of A with respect to B, ${{v}_{AB}}=\sqrt{{{10}^{2}}+{{10}^{2}}}=10\sqrt{2}$
From the above diagram the shortest distance between ships A and B is PQ.
Consider triangle POQ,
$\sin 45=\dfrac{PQ}{OQ}$
$OQ=100km$
Then,
$PQ=OQ\times \sin 45=100\times \dfrac{1}{\sqrt{2}}=50\sqrt{2}m$
We have, $\text{time = }\dfrac{\text{distance}}{\text{velocity}}$
Substitute the values of PQ and ${{v}_{AB}}$in the above equation, we get,
Then, the time taken to reach the shortest distance,
$t=\dfrac{PQ}{{{v}_{AB}}}=\dfrac{50\sqrt{2}}{10\sqrt{2}}=5h$

Therefore, the answer is option B.

Note:
Alternate method to solve the question

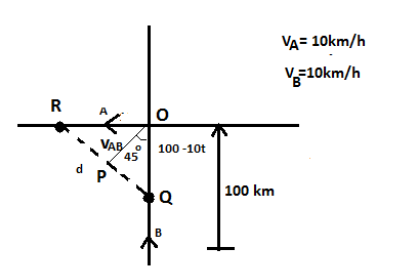
Given,
Velocity of A, ${{v}_{A}}=10km/h$
Velocity of B, ${{v}_{B}}=10km/h$
Given that, both ships A and B are travelling with the same velocity. Then, at any instant $t$ the distance traveled by the ships will be the same.
i.e.,
Distance travelled by ship A = Distance travelled by ship B $=10t$
Then, the remaining distance for B is, $100-10t$.
Then, considering triangle ROQ,
${{d}^{2}}=P{{O}^{2}}+O{{Q}^{2}}$
${{d}^{2}}={{\left( 10t \right)}^{2}}+{{\left( 100-t \right)}^{2}}$
$d=\sqrt{100{{t}^{2}}+10000+100{{t}^{2}}-200t}=\sqrt{200{{t}^{2}}+10000-2000t}$
Differentiating both sides with respect to time,
$\dfrac{d\left( d \right)}{dt}=0$
$\Rightarrow 0=400t-2000$
$\Rightarrow 400t=2000$
$\Rightarrow t=5hr$