Question

A shell projected from a level ground has a range R if it did not explode. At the highest point, the shell explodes into two fragments having masses in the ratio 1:3 with each fragment moving horizontally immediately after the explosion. If the lighter fragment falls at a distance R from the point of projection, behind the point of projection, the distance at which the other fragment falls from the point of projection is
A. $\dfrac{3R}{8}$
B. $\dfrac{R}{2}$
C. $\dfrac{5R}{3}$
D. $\dfrac{3R}{4}$

Answer 1

By using the given ratio of the fragments and the fact that their sum will give the initial mass of the shell before explosion we could find the masses of fragments in terms of the initial mass of the shell. Then you could substitute this in the expression for centre of mass along with the distances. Be careful about the position of centre of mass.

Formula used:
Centre of mass,
${{X}_{CM}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}$

Complete Step by step solution:
In the question we are given a shell that has range R when projected without getting exploded. At the maximum height of the projectile, explosion occurs in the ratio 1:3. The lighter particle is known to fall at distance R behind the point of projection and we are asked to find the distance at which the other fragment falls from the point of projection.

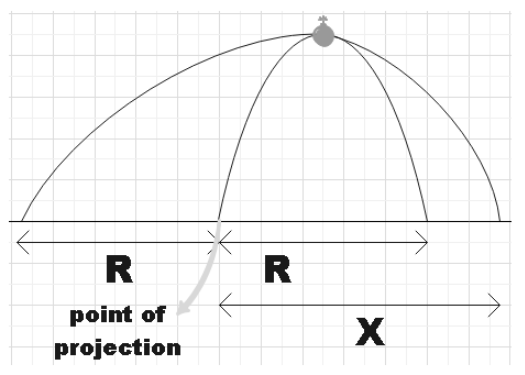
Let the mass of the first fragment be ${{m}_{1}}$ and that of the other be ${{m}_{2}}$. Then,
${{m}_{1}}+{{m}_{2}}=M$ …………………………………. (1)
Where, M was the mass before explosion.

The falling of explosion of fragments will be in such a way that assures the centre of mass to be on the range R. Let, X be the distance that other fragments falls, then,
${{X}_{CM}}=R$ …………………………………………………….. (2)
${{X}_{CM}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}$ …………………………………………… (3)

We are given the ratio of the masses to be,
$\dfrac{{{m}_{1}}}{{{m}_{2}}}=\dfrac{1}{3}$ ………………………………………………… (4)

From (1) and (4),
${{m}_{1}}=\dfrac{M}{4}$ ………………………………………………… (5)
${{m}_{2}}=\dfrac{3M}{4}$ ………………………………………………… (6)

Substituting (5), (6) and (2) in (3) we get,
$R=\dfrac{\left( \dfrac{M}{4} \right)\left( -R \right)+\dfrac{3M}{4}X}{M}$
$\Rightarrow 4R=-R+3X$
$\therefore X=\dfrac{5R}{3}$

Therefore, we found that the second fragment falls at a distance of $\dfrac{5R}{3}$ from the point of projection.

Hence, option C is found to be the correct answer.

Note:
The centre of mass will remain at rest or continue its uniform motion in the absence of an external force. The centre of mass will accelerate in the presence of a force and the acceleration is given by Newton’s second law. For the case of explosion the centre of mass will trace the same path it would have taken in the absence of that explosion. This is because an explosion doesn’t involve any external forces but internal forces.