Question

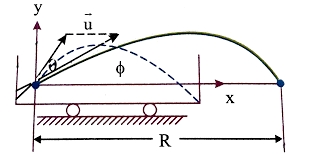
A shell is projected from a gun with a muzzle velocity $u$ . The gun is fitted with a trolley car at an angle $\theta$ as shown in Figure. If the trolley car is made to move with constant velocity $v$ towards right. Find the
(a) Horizontal range of the shell relative to ground.
(b) Horizontal range of the shell relative to a person travelling with a trolley.

Answer 1

In order to solve this kind of question, we will be using the concept of kinematics. We will discuss the motion of an object in projectile motion. We will also be using the concept of relative motion in a plane.
The second equation of motion $s=ut+\dfrac{1}{2}a{{t}^{2}}$
Where $u$ is the initial velocity, $s$ is the distance covered, $a$ is the acceleration and $t$ is the time taken.

Complete step by step answer:
As we can conclude from the figure, the shell which is fired from the gun will travel in a projectile motion in the direction of projection. Now what do we mean when we say that the shell is in a projectile motion? It means that the shell will travel in a curved path with reference to the ground.
The point from which the shell is projected is known as the point of projection and, and the angle with which the projected shell is projected with respect to the point of projection is known as the angle of projection. After the shell is projected, the shell will travel in a curved path for a certain distance and then fall on to the ground. The horizontal distance travelled by the shell on the ground is known as the horizontal range or the range of the shell. And lastly, the total time taken by the shell to travel this distance is known as the time of flight.
According to the figure, we can see that the particle will perform a parabolic path for the observer on the trolley as well as for the observer who is standing on the ground. And also that the gun firing the shell is fitted on a trolley car which is also moving with some velocity with respect to the ground.
Now to solve the question, we will be considering two different cases:
CASE 1: (the observer is standing on the ground)
In this case, the observer is standing on the ground and he can see the trolley moving with some velocity and a shell is projected through a gun fitted on this trolley. Therefore, the data we can write is as follows:
The velocity of trolley is ${{v}_{t}}$
The velocity of the shell when it was projected with respect to the ground is
${{\vec{v}}_{s}}=\vec{u}+{{\vec{v}}_{t}}$ ,
where $u$ is the velocity of the projection of the shell with respect to the trolley. Writing IN terms of components, we get
$\begin{aligned} & {{{\vec{v}}}_{s}}=u\cos \theta \hat{i}+u\sin \theta \hat{j}+v\hat{i} \\\ & \Rightarrow {{{\vec{v}}}_{s}}=(u\cos \theta +v)\hat{i}+u\sin \theta \hat{j} \\\ \end{aligned}$
Now, to calculate the horizontal distance travelled by the shell or its range, we use the law of kinematics, i.e.,
$\vec{s}={{\vec{v}}_{s}}t+\dfrac{1}{2}\vec{a}{{t}^{2}}$
$\Rightarrow \vec{s}=[(u\cos \theta +v)\hat{i}+u\sin \theta \hat{j}]t+\dfrac{1}{2}g{{t}^{2}}\hat{j}$
Where acceleration $a$ is taken to be the gravitational acceleration $g$ due to the earth which is acting in the Y direction.
$\Rightarrow \vec{s}=(u\cos \theta +v)t\hat{i}+(ut\sin \theta +\dfrac{1}{2}g{{t}^{2}})\hat{j}$
Now, as we want to calculate the maximum horizontal distance covered by the shell, the y-component would be zero. Therefore, comparing the components on both sides of
$s\hat{i}+s\hat{j}=(u\cos \theta +v)t\hat{i}+(ut\sin \theta +\dfrac{1}{2}g{{t}^{2}})\hat{j}$
Hence,
$s=(u\cos \theta +v)t$ …(A)
and
$0=ut\sin \theta +\dfrac{1}{2}g{{t}^{2}}$
$\Rightarrow t=\dfrac{2u\sin \theta }{g}$ …(B)
Placing the value of time in equation (A) from equation (B), we get
$s=(u\cos \theta +v)(\dfrac{2u\sin \theta }{g})$
The above equation shows the horizontal range of the shell with respect to the ground.
CASE 2: (the observer is standing on the trolley)
If the observer is standing on the trolley, then
The velocity of the shell with respect to the trolley is ${{\vec{v}}_{s}}=\vec{u}=u\cos \theta \hat{i}+u\sin \theta \hat{j}$
Using similar formulae as of the first case
$\vec{s}={{\vec{v}}_{s}}t+\dfrac{1}{2}\vec{a}{{t}^{2}}$
$\Rightarrow \vec{s}=ut\cos \theta \hat{i}+(ut\sin \theta +\dfrac{1}{2}g{{t}^{2}})\hat{j}$
Comparing the components similar to the first case for
$s\hat{i}+s\hat{j}=ut\cos \theta \hat{i}+(ut\sin \theta +\dfrac{1}{2}g{{t}^{2}})\hat{j}$
Hence,
$s=ut\cos \theta$ -(C)
and
$0=ut\sin \theta +\dfrac{1}{2}g{{t}^{2}}$
$\Rightarrow t=\dfrac{2u\sin \theta }{g}$ -(D)
Placing the value of time in equation (D) from equation (C), we get
$\begin{aligned} & s=(u\cos \theta )(\dfrac{2u\sin \theta }{g}) \\\ & \Rightarrow s=\dfrac{2{{u}^{2}}\sin \theta \cdot \cos \theta }{g} \\\ & \Rightarrow s=\dfrac{{{u}^{2}}\sin 2\theta }{g} \\\ \end{aligned}$
Lastly, the above equation shows the horizontal distance covered by the shell or the range of the shell with respect to the observer standing on the trolley.

Note:
Keep in mind the frame of reference by which the velocity is to be calculated and also don’t forget to write the velocities in the form of components as the direction in which the shell is projected is in a two-dimensional plane.