Question

A shell fired from the ground is just able to cross in a horizontal direction the top of a wall $90m$ away and $45m$ high. The direction of projection of the shell will be
$\left( A \right)25^\circ$
$\left( B \right)30^\circ$
$\left( C \right)45^\circ$
$\left( D \right)none\,\,of\,these$

Answer 1

First of all we have to draw a rough diagram showing all the required parameters to analyze the problem. From the formula of projectile motion we can use the maximum height formula and the range of the projectile motion in the next step. Now taking the ratio of the two parameters we can find the direction of projection of the shell which is the horizontal angle made by the shell.

Complete answer:
As from the given problem we have a shell fired from the ground that is just able to cross in a horizontal direction the top of a wall $90m$ away and $45m$ high.

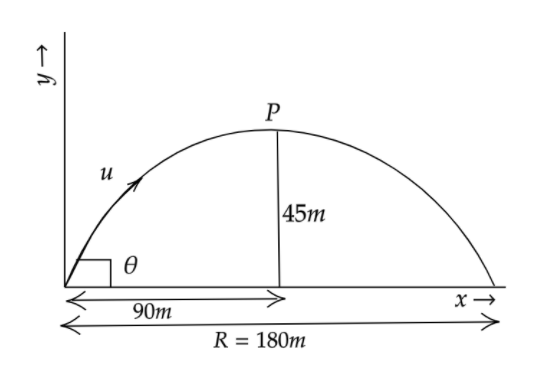
Here in the figure the point P represents the highest point that is of the height of the wall which is equals to $45m$. And the distance of the height point from the starting point is $90m$. Hence the double its distance equals the range of the projectile motion which is $R = 2 \times 90m = 180m$.
Now using the projectile motion formulas we have,
Height H equal to,
$H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$
Where,
The initial velocity at which the shell is fired is equal to u.
The horizontal angle made by the shell equal to $\theta$.
The acceleration due to gravity on the fired shell is $g$.
Now we know the height of the wall or we can say the highest point of the projectile motion is $45m$.
Hence,
$45m = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}} \ldots \ldots \left( 1 \right)$
Horizontal range R is equal to,
$R = \dfrac{{{u^2}\sin 2\theta }}{g}$
Where,
The initial velocity at which the shell is fired is equal to u.
The horizontal angle made by the shell equal to $\theta$.
The acceleration due to gravity on the fired shell is $g$.
We also know the value of the range of the projectile motion as $180m$.
Hence,
$180m = \dfrac{{{u^2}\sin 2\theta }}{g} \ldots \ldots \left( 2 \right)$
Dividing equation $\left( 2 \right)$ by equation $\left( 1 \right)$, we get
$\dfrac{{180m}}{{45m}} = \dfrac{{\dfrac{{{u^2}\sin 2\theta }}{g}}}{{\dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}}}$
Cancelling the common terms we will get,
$4 = \dfrac{{2\sin 2\theta }}{{{{\sin }^2}\theta }}$
We know, $\sin 2\theta = 2\sin \theta \cos \theta$
So,
$4 = \dfrac{{2 \times 2\sin \theta \cos \theta }}{{{{\sin }^2}\theta }} = \dfrac{{4\cos \theta }}{{\sin \theta }}$
Now on further solving and putting $\dfrac{{\sin \theta }}{{\cos \theta }} = \tan \theta$ we will get,
$\tan \theta = 1 \Rightarrow \theta = {\tan ^{ - 1}}1$
Hence the direction of projection of the shell will be $\theta = 45^\circ$.
Therefore the correct option is (C).

Note: Remember that in a projectile motion there are two simultaneous independent rectilinear motions one is along the x- axis which is responsible for the horizontal motion of the particle and the other is along the y-axis which is responsible for the vertical motion of the particle. X-axis is a forward motion while y-axis is a downward motion of a particle.