Question

A series R - L - C $\left( R=10\Omega ~,{{X}_{L}}=20\Omega ,{{X}_{c}}=20\Omega \right)$ circuit is supplied by $V=\sin \omega t\text{ Volt}$ then power dissipation in circuit is,
$\text{A}\text{. Zero Watt}$
$\text{B}\text{.10 Watt}$
$\text{C}\text{. 5 Watt}$
$\text{D}\text{. 2}\text{.5 Watt}$

Answer 1

Power dissipated in a R-L-C circuit can be expressed in terms of rms current and voltage.
When ${{X}_{L}}={{X}_{C}}$ resonance occurs in the RLC circuit .Then the impedance of the R-L-C circuit will be equal to the value of resistance connected to that circuit.
Formula used:
$\text{Power dissipated, P = }{{\text{i}}_{rms}}{{E}_{rms}}\cos \Phi$
$\tan \Phi =\dfrac{{{X}_{L}}-{{X}_{C}}}{R}$
${{I}_{rms}}=\dfrac{{{I}_{o}}}{\sqrt{2}}$
${{E}_{rms}}=\dfrac{{{E}_{o}}}{\sqrt{2}}$
${{V}_{rms}}=\dfrac{{{V}_{o}}}{\sqrt{2}}$
$P=\dfrac{V_{rms}^{2}}{{{Z}^{2}}}R$

Complete answer:
Let us draw the R-L-C diagram,

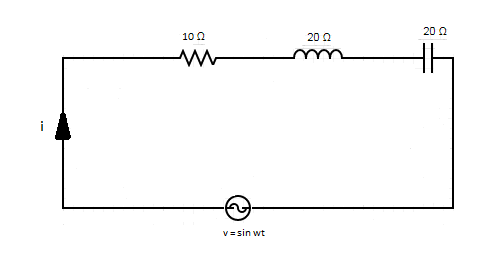
Given,
$R=10\Omega$
${{X}_{L}}=20\Omega$
${{X}_{c}}=20\Omega$
$V=\sin \omega t\text{ Volt}$
$\text{Power dissipated, P = }{{\text{i}}_{rms}}{{E}_{rms}}\cos \Phi$ ------ 1
Here${{X}_{L}}={{X}_{c}}=20\Omega$,
Hence the impedance diagram can be drawn as
Therefore,
$\text{Impedance, Z=R}$ ------ 2
The phase angle between the voltage and current is represented by $\Phi$. The tangent of this angle is given by,
$\tan \Phi =\dfrac{{{X}_{L}}-{{X}_{C}}}{R}$
Substitute the values of ${{X}_{L}}$,${{X}_{C}}$, $R$
We get,
$\tan \Phi =\dfrac{20-20}{10}=0$
$\Phi =0$
Then,
$\cos \Phi =\cos 0=1$ ------- 3
Now, we need to find the values of${{\text{i}}_{rms}}\text{ and }{{E}_{rms}}$.
${{i}_{0}}=\dfrac{{{V}_{0}}}{Z}=\dfrac{10}{R}=\dfrac{10}{10}=1A$
Then,
${{\text{i}}_{rms}}\dfrac{{{I}_{o}}}{\sqrt{2}}=\dfrac{1}{\sqrt{2}}A$ --------- 4
${{E}_{rms}}\dfrac{{{E}_{o}}}{\sqrt{2}}=\dfrac{10}{\sqrt{2}}V$ ----------5
Substitute equations 3, 4, and 5 in equation 1
$\text{Power dissipated, P= }{{\text{i}}_{rms}}{{E}_{rms}}\cos \Phi$
$P=\dfrac{1}{\sqrt{2}}\times \dfrac{10}{\sqrt{2}}\times 1=\dfrac{10}{2}=5W$

So, the correct answer is “Option C”.

Note:
Alternate method to solve the question.
We have power dissipation,
$P=\dfrac{V_{rms}^{2}}{{{Z}^{2}}}R$ --------- 1
${{V}_{rms}}=\dfrac{{{V}_{0}}}{\sqrt{2}}=\dfrac{10}{\sqrt{2}}$ ---------- 2
Here, $Z=R=10$ --------- 3
Substituting equation 2 and 3 in equation 1.
$P=\dfrac{{{\left( \dfrac{10}{\sqrt{2}} \right)}^{2}}}{{{10}^{2}}}\times 10=\dfrac{500}{100}=5W$