Question

A series-parallel combination of a battery consisting of a large number $N = 300$ of identical cells, each with an internal resistance $r = 0.3\,\Omega$, is loaded with an external resistance $R = 10\,\Omega$ then, the number $n$ of parallel group consisting of an equal number of cells connected in series at which the external resistance generates highest thermal power is
A. 3
B. 4
C. 5
D. none of the above

Answer 1

First derive the relation between the total number of cells, internal resistance and the number of rows. Determine the current flowing through each row. Then consider a loop in which the cells are connected in series which is connected to the external resistance. Apply Kirchhoff’s voltage law to this loop and determine the value of current. Then derive the relation for the power generated. Use the condition for the generation of the thermal power and determine the number of groups in which the cells should be divided.

Formula used:
The power $P$ generated in a circuit is given by
$P = {i^2}R$ …… (1)
Here, $i$ is the current and $R$ is the resistance.

Complete step by step answer:
We have given that the total number of cells is $300$.
$N = 300$
The internal resistance of each cell is $0.3\,\Omega$ and the external resistance connected in an external circuit is $10\,\Omega$.
$r = 0.3\,\Omega$
Let $x$ be the number of cells connected in $n$ rows in the circuit. Then we can write
$N = xn$
$\Rightarrow x = \dfrac{N}{n}$
Let $i$ be the current in the external resistor. Then the current through each parallel row will be $\dfrac{i}{n}$. Let us consider one loop of the circuit in which the external resistor is connected.

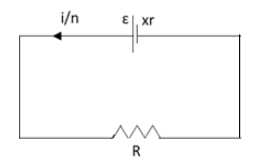
Let us apply Kirchhoff’s voltage law to this loop.
$iR + \dfrac{i}{n}xr - x\varepsilon = 0$
$\Rightarrow i\left( {R + \dfrac{{xr}}{n}} \right) - x\varepsilon = 0$
$\Rightarrow i = \dfrac{{x\varepsilon }}{{R + \dfrac{{xr}}{n}}}$
Substitute $\dfrac{N}{n}$ for $x$ in the above equation.
$\Rightarrow i = \dfrac{{\dfrac{N}{n}\varepsilon }}{{R + \dfrac{{\left( {\dfrac{N}{n}} \right)r}}{n}}}$
$\Rightarrow i = \dfrac{{\dfrac{N}{n}\varepsilon }}{{R + \dfrac{{Nr}}{{{n^2}}}}}$
The thermal power in the circuit is given by equation (1).
Substitute $$$$ for $i$ in equation (1).
$P = {\left( {\dfrac{{\dfrac{N}{n}\varepsilon }}{{R + \dfrac{{Nr}}{{{n^2}}}}}} \right)^2}R$
The power generated will be maximum if
$\dfrac{{dP}}{{dn}} = 0$

Substitute ${\left( {\dfrac{{\dfrac{N}{n}\varepsilon }}{{R + \dfrac{{Nr}}{{{n^2}}}}}} \right)^2}R$ for $P$ in the above equation.
$\dfrac{{d\left[ {{{\left( {\dfrac{{\dfrac{N}{n}\varepsilon }}{{R + \dfrac{{Nr}}{{{n^2}}}}}} \right)}^2}R} \right]}}{{dn}} = 0$
$\Rightarrow\dfrac{{\dfrac{N}{n}\varepsilon \dfrac{{d\left( {R + \dfrac{{Nr}}{{{n^2}}}} \right)}}{{dn}} - \left( {R + \dfrac{{Nr}}{{{n^2}}}} \right)\dfrac{{d\left( {\dfrac{N}{n}\varepsilon } \right)}}{{dn}}}}{{{{\left( {R + \dfrac{{Nr}}{{{n^2}}}} \right)}^2}}} = 0$
$\Rightarrow \dfrac{N}{n}\varepsilon \dfrac{{d\left( {R + \dfrac{{Nr}}{{{n^2}}}} \right)}}{{dn}} - \left( {R + \dfrac{{Nr}}{{{n^2}}}} \right)\dfrac{{d\left( {\dfrac{N}{n}\varepsilon } \right)}}{{dn}} = 0$
$\Rightarrow \dfrac{N}{n}\varepsilon \left( { - \dfrac{{2Nr}}{{{n^3}}}} \right) - \left( {R + \dfrac{{Nr}}{{{n^2}}}} \right)\left( { - \dfrac{N}{{{n^2}}}\varepsilon } \right) = 0$
$\Rightarrow \dfrac{{2{N^2}\varepsilon r}}{{{n^4}}} = \left( {R + \dfrac{{Nr}}{{{n^2}}}} \right)\left( {\dfrac{N}{{{n^2}}}\varepsilon } \right)$
$\Rightarrow \dfrac{{2Nr}}{{{n^2}}} = R + \dfrac{{Nr}}{{{n^2}}}$
$\Rightarrow \dfrac{{Nr}}{{{n^2}}} = R$
$\Rightarrow n = \sqrt {\dfrac{{Nr}}{R}}$
Substitute $300$ for $N$, $10\,\Omega$ for $N$ and $0.3\,\Omega$ for $n$ in the above equation.
$\Rightarrow n = \sqrt {\dfrac{{\left( {300} \right)\left( {0.3\,\Omega } \right)}}{{10\,\Omega }}}$
$\Rightarrow n = \sqrt 9$
$\therefore n = 3$
Therefore, the number of parallel groups is $3$.

Hence, the correct option is A.

Note: The students may think that how we have calculated the value of the current flowing in each loop of the cells connected in series. But the students should keep in mind that the group of cells connected in series are parallel to each other and in a parallel circuit current divides equally. Hence, we have divided the total current in the external circuit by the number of rows in parallel.