Question
Question: A series LCR circuit with \[L=4.0\], \[C=100\mu F\], \[R=60\Omega \] connected to a variable frequen...
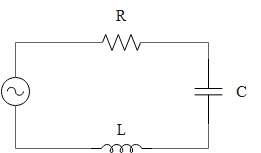
A series LCR circuit with L=4.0, C=100μF, R=60Ω connected to a variable frequency 240V source as shown in figure calculate:
(i) the angular frequency of the source which drives the circuit resonance,
(ii) the current at the resonating frequency,
(iii) the rms potential drop across the inductor at resonance.
Solution
This is a direct numerical question. To find the angular frequency, we will use the inductance and the capacitance values. To find the current, we will use the emf value and the resistance and to find the rms potential drop, we will use the current and the inductive reactance values.
Formula used:
ω=LC1
I=Rε
VL=IXL
Complete step-by-step answer:
From the given question statement, we have the data as follows.
The inductance, L=4.0
The capacitance, C=100μF
The resistance, R=60Ω
The emf, ε=240V
(i) The angular frequency of the source which drives the circuit resonance.
Consider the formula to compute the value of the angular frequency.
ω=LC1
Where L is the inductance and C is the capacitance.
Substitute the values in the above formula
ω=4×100×10−61
Therefore, the value of the angular frequency is, ω=50rad/s.
(ii) The current at the resonating frequency
Consider the formula to compute the value of the current.
I=Rε
Where ε is the emf and R is the resistance.
Substitute the values in the above formula
I=60240
Therefore, the value of the current is, I=4A.
(iii) The rms potential drop across the inductor at resonance
Consider the formula to compute the value of the rms potential drop.
& {{V}_{L}}=I{{X}_{L}} \\\ & {{V}_{L}}=I\omega L \\\ \end{aligned}$$ Where $$I$$ is the current, $$L$$ is the inductance, $$\omega $$ is the angular frequency and $${{X}_{L}}$$ is the inductive reactance. Substitute the values in the above formula $${{V}_{L}}=4\times 50\times 4$$ Therefore, the value of the rms potential drop is, $${{V}_{L}}=800\,V$$. $$\therefore $$ The values of the angular frequency, current and rms potential drop are $$50\,{rad}/{s}\;$$, $$4\,A$$ and $$800\,V$$. **Note:** As in the question statement, the units of the parameters is given in terms SI units, so, no need to change them. The formula for computing the inductive reactance should be known. Here, in this question, the variable frequency refers to the emf value.